Monday, April 30, 2007
BOB version 5.0
BOB THE BUILDER :))
REMEMBER
PERMUTATIONS concern arrangements or choices that regard a significance in the change of the order.
COMBINATIONS concern arrangements that do NOT regard a significance in the change of order.
Taken off MrSiwWy's bob.
BOB 5
Toodle-loo Kangaroo.
The Bob that almost never was...
The unit of counting presented a very different view upon how we approach mathematics. Before, we always just applied formulas very directly and precisely, but here we must think first. I think that DEV really distorted my homework endeavors by consuming all of my time, thus leaving no time for any exercises. I really regret not doing any exercises, as I suffered greatly when each of those grueling quizzes were presented to us (GRr my Averaggee )= ) and now I feel so horrible. Though, now that I look back at the entire unit I can see that it's not actually that difficult if you familiarize yourself with the methods of thinking. Each question almost always requires a unique approach But, like Mr. K said, try to associate or relate the problem at hand with questions that we have conquered together throughout the unit. It's a good tip, and there's quite a bit to remember and methods of solving that I know I wil(as should all of you) practice to prepare for this test. Remember, permutations concern arrangements or choices that regard a significance in the change of the order, whereas combinations concern arrangements that do NOT regard a significance in the change of order. Well I have to go catch up on all my english homework (Grr DEV), hope my computer doesn't go sour again anytime soon, and I also hope to have time to review efficiently for tomorrow's test. Boo for the deadly combination of a bombardment of homework and uncooperative computer =/ Hope you all can study and do your best on the approaching counting test! Hope I get the chance to study =) G'night!
BOB the Snail
I hope everyone will study hard for the dreadful test. =D
Today's Slides: April 30
To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.
Scribe Post: Preparing for the Counting Test
Reminder: YOU CAN, I repeat, YOU CAN EDIT your DEV projects if you already published your projects.
Morning Class:
This morning, we had our pre-test. Here are the answers.
1. 7 teams compete in a men's hockey league. If each team plays each other twice, how many games are necessary to complete the league schedule?
Solution:

2. The sum of the seventh row of Pascal's triangle is the same solution to;
Solution:
Since the 7th row in Pascal's Triangle is 64, which is the same as 2^6, we need to find which of these choices have the same answer...
 Since (b) is 2^6, the answer is (b).
Since (b) is 2^6, the answer is (b).3. Suppose the last four digits of a telephone number must include at least one repeated digit. How many such numbers are there?
Solution:

4. A multiple choice exam has 20 questions, each with four possible answers, and 10 additional questions, each with five possible answers. How many different answer sheets are possible?
Solution:
 5. In a 52 card deck, how many 5 card poker hands are possible that have exactly two pair? one pair?
5. In a 52 card deck, how many 5 card poker hands are possible that have exactly two pair? one pair?Solution:
 That's all we did this morning...
That's all we did this morning...Afternoon Class:
This afternoon, we did our usual group workshops...
Here are the questions:
1.

2.

3.
 * the first digit is 9 in (a) because we can't use 0 as a first number. That would make it a 2 digit number instead. (eg. 024)
* the first digit is 9 in (a) because we can't use 0 as a first number. That would make it a 2 digit number instead. (eg. 024)* the first number is 8 in (b) because we already used a number for the last one to make the digit odd. The next choice is 8 again because this time, we included 0.
* The first solution is for the digit to end in 5, the 2nd solution is for the digit to end in 0. (Both are divisible by 5) For the 2nd solution, the first number is 9 because 0 is in the last digit already, so we don't have to restrict it for the first number.
4.
 * In (a), the answer is 7! because we don't care about the order of the books.
* In (a), the answer is 7! because we don't care about the order of the books.* In (b), the answer is 5!3! because if we put the 3 French books in a bag, it is considered as "1". Therefore we have 5 objects to arrange. (5!) After that we remove the 3 books from the bag and multiply 3! to the answer. The 3 books can be arranged in 3 different ways.
* In (c), the question is similar to the "word" problems. Since there are 4 similar objects, they are non-distinguishable.
5.

6.

7.

8.

9.

Reminder: There is no, I repeat, NO test tomorrow because of a multimedia presentation at the gym.
Well... That's all we did for the day. I hope everything was clear. Next scribe is... Grey-M! =D
Sunday, April 29, 2007
How many ways can BOB be arranged so that....
Well maybe not this test. Feel pretty good but there are so many little itty-bitty things that catch me everywhere.
Good luck all!
Grey-M
BOBING FOR MATH
-SAMUS
BOB

There was some what unsuspected quizzes !!! I think I've clearly understand through this unit really quickly but . If the test is as simple as the quizzes, well I should do fine but i be freezing in some question and be confused between nPr and nCr? I myself am tired of getting confused, so I'm studying all tonight and maybe Monday night if i get the chance. If I don't get at least an higher mark, I'm gonna be some down and pissed off. I hope you all do great in the pre-test and test as well. Good luck to everyone.
BEE OH BEE number five.

SCRIBE
April 26TH 2007
MORNING:
First thing we started off with was a quiz that was on counting. The first question dealt with 3 positions with ten people and how they are arranged. we came up with 10*9*8 because there are ten people that can have one position, after that nine people can be assigned the second position since one is already assigned. And 8 because there are 8 people that can be in the third position. The second question was about how many words can be generated with the word CALCULUS. Since there are 8 letters it should be 8! However, there are two L's, two U's, and two C's which are all non-distinguishable objects because we can't tell the difference between the doubles. So, it is 8!/ 2!2!2!. 2! are the U's, L's, and C's since we can't tell them apart. Question 3 the answer is (7-1)! which is equivalent to 720. That's because since 7 people are sitting in a circle and one person could be the point so 6 others sit around. Question 4 the answer is 4!2!2!2!2! because there are four couples that could be arranged and two people in the four couples and they too can be rearranged. The answer for question five is 1152 because if the men and women alternate then it would look like this
..............................................................................
..............................................................................
JANN
BOB TIME
This unit included its share of interesting and difficult times. I must agree with Mr. K that homework was definitely essential for this unit, in my opinion. Most of the questions had their own elements that may have related to other questions but were not exactly the same.
I find that the most difficulties I have with this unit is the race against time. There are so many ways to think about each question that it seems as though I'm playing against time to find the path that will lead me to the solution.
Also, besides the more simple combinatorics word problems, I don't think that I'm extremely comfortable with the binomial theorem yet. Only time will tell because I have yet to finish my homework and we still have pretest day tomorrow.
Well that's all I have to reflect on, Good luck to everyone on the Pre-test and Test this week!
Saturday, April 28, 2007
BOB your heart out

Friday, April 27, 2007
BOB-ing 5
WOW! Another BOB! This only means one thing. TEST!!!! Gee.. This unit has been different. I've had so many confusions with this one. There's a pick formula, choose formula. Those words are synonymous! LOL! Maybe... So yeah. The binomial Theorem startled me in the beginning but I know that with a few more practice, I will be comfortable with this! But, my quizzes have been lower than what I used to get. It's all of these DEV stuff that stress me out. I couldn't do my homework because of that! Anyway, Permutations and combinatorics are easy. It's just the matter of remembering which is which, which formula to use, in which circumstances! WOW! That's hard! Nevermind. So is anyone ready for the test? I'm not. To tell you the truth, I don't feel good about it. Pre-emptively, I will feel something about an upcoming test and for this one, I know it wouldn't be a good one. Sad... So, instead of rambling all over the place here, I should continue my DEV project! It's due on Monday! See you guys! I'm out!
Thursday, April 26, 2007
Today's Slides: April 26
Here they are ...
To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.
Wednesday, April 25, 2007
Scribe
The Day our Minds were Blown...(swish)
First, Mr. K promised and reassured us that he was going to blow our minds and show us one way the universe was built, but before that he explained the meaning of "Tedious" to Jojo and whoever else that didn't know the meaning.
Tedious: Tiresome by reason of length, slowness, or dullness; boring.
Binomial Theorem
Mr. K told us to expand and simplify the following:
(a+b)0
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
After solving the first 5 questions simply using the FOIL method or the short way, he then showed us the PASCAL's Triangle...
The pattern is shown in the red arrows/lines, you must find the sum of the two numbers in the previous row to get the numbers in the next row.
Okay, not watch this carefully...
Patterns in...
The Coefficient: Adding the two coefficients from the row above.(seen in the Pascal's Triangle)
A: Decreasing by (a n - 1 ), (a n - 2 ), (a n - 3 )...
B: Increasing by (b n + 1 ), (b n + 2 ), (b n + 3 )...
Later on, Mr. K gave us the same triangle and told us to find patterns in the triangle , and we found a number of different ones:
Regular counting numbers
The Sum of Counting numbers a.k.a. "triangular numbers"
Sum of Triangular numbers
powers of 11
Fibonacci Sequence
Leonardo Fibonacci was an French/Italian mathematician...More Info.
the sequence is: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89... (you get the next number by finding the sum of the two previous numbers). As you can see this sequence appears in Pascal's Triangle and in a lot of the natural living things on earth such as plants, bee's, flowers, even in a Leonardo Da Vinci painting. He was also explaining how "Phi" was in the sequence and how it's in everything from 4x6 pictures and our body's to what we consider beautiful, and then the bell rang...
The next scribe will be....
i haven't decided yet i will get back to you... Good Nite!
Today's Slides and Homework: April 25
To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.
Here is your homework assignment:

and here are the answers ...

Tuesday, April 24, 2007
Then Mr. K told us we will be talking about poker hands and everyone started talking to each other about the game of poker. We talked and had to solve all the hands possible in the game of poker like how many possible way are there to get a royal flush, only 4 ways to can get that hand. Then continuing on with the straight flush then with the 4 of a kind, then full house.
In the afternoon class we split into groups to solve the last few questions so, move with the regular flush, then the straight but not the same suits, then 3 of a kind and two pairs. Mr.K gave a question on how many games have to be played if a 10 team conference have to play each other team once so, 10 C 2=45 or the easy way, 9x8x7x6x5x4x3x2x1=45. The next question deals with a group of seven people reach a fork on the road and how many can be made that four people has to go one way and the others go to the other path, so we started of by 7 C 4 X 3 C 3 (because theres a full group of 7 people and 4 of them has to go to that path then there were only 3 people left to go to that path). It was near the end of class so Mr. K told the homework was to find the last to hands in the poker game one set of pair and no pairs at all
link --> href="http://www.slideshare.net/dkuropatwa/precal-40s-slides-april-24-2007/1"
The Scribe That Almost Wasn't
MONDAY, after Mr. K was finished preparing the days lesson we got right to work.
He hit us with a question:
a) How many ways can the ways GEOMETRY be arranged so that vowels and consonants alternate?
 First we give 8 available spaces labeled cvcvcvcv because the vowels an consonants alternate.
First we give 8 available spaces labeled cvcvcvcv because the vowels an consonants alternate. YES, in this case Y is a vowel !!!!!!!!!!!!!!!!!!!!!!!!!!!
There are four vowels and consonants so in the first space there are 4 available consonants, in the second there are 3 in the third there are 2 and in the last space there is only 1 consonant available so therefore is labeled one. Same pattern applies to the vowels.
In the above illustration there are two sets because you could either start with a vowel or start with a consonant.
Then you mulitply:
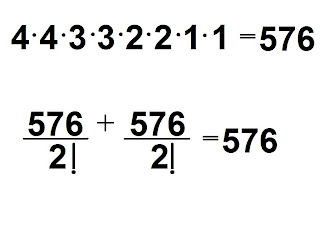 Note: you add 576 two times because there are two sets.
Note: you add 576 two times because there are two sets.b) How many ways is y the last letter?

Quest. 2
How many ways can student council choose a subcommittee of 5 people from the entire council which consist of 11 people?

Comination: An arrangement of objects where order does not matter.
 Given a set of n objects, how many different groupls of n objects can be chosen were order doesn't matter.
Given a set of n objects, how many different groupls of n objects can be chosen were order doesn't matter.For example:
How many different tickets can be sold in the 6/49?
(Basically just plug in the numbers)
To punch this in your calculator
Press the MATH button
Choose the PRB
Choose the third choice which is n choose r

In other words, you much better off just saving your money!!!!!!!
I'm still in the learning process for these blogs, as you can tell I'm not that great, but i hope i covered everything. Until my next duty this is got MELk out.
Today's Slides: April 24
To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.
Monday, April 23, 2007
Today's Slides: April 23
To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.
Saturday, April 21, 2007
Counting
MORNING:
At the beginning of class we talked about different things we could do for our DEV Projects. To make fancy fractions like Mr. K makes on Apple Works, you can either download MathType or you can use Microsoft Word. Personally, I use Microsoft Word 2007, but I'm not sure if the older versions can do that as well. To upload photos you can use Flickr, most of you know about Photobucket, there's also Fileden, Freewebtown and Prizaar.
Then we started with our lesson!

Follow the butterflies!
You need to make a four letter word. So basically there's 7 letters you can use all together. The first letter you have 7 options to pick from, then one is being used so for the next spot you only have 6 options. Then the next is 5 options and then 4 options.
The red answer is the correct answer. At the beginning there has to be a vowel and at the end there has to be a consonant. Regardless of which letters those are, there a two letters that have to be in each spot. Which means, there's only 5 letters that can go in the second spot and 4 in the other since two are already being used.
Out of the 7 letters, there are 3 consonants and 4 vowels. To make them alternate they either have to be vowel, consonant, vowel, consonant or consonant, vowel, consonant, vowel. So, for the first, once 1 vowel is used the third letter only has 3 options left. Same goes for the consonants, once one consonant is used, there's only 2 options left. Once you've figured it out, you add the two together and it gives you your answer.

When it comes to circles things change a bit. To break it down, the order in which people or objects are placed around a table is the only thing that matters. Rotating them doesn't make a different, frankly they're just in a different position around the table with the exact SAME order. The same person will be on their right and the same person will be on their left. So for these kind of questions the formula to find it is (n-1)! (Where "!" means Factorial not "I really, really mean it"). On this slide the circles in RED are the same and the circles in BLUE are the same.
HOWEVER... tables are different from bracelets. With bracelets, you're able to turn them over. So technically each arrangement actually represents 2 of them. The same applies for necklaces and other things that can be flipped. In these special cases, the formula you use is (n-1)!/2.

With this questions, you can pretty much treat the married couples as ONE person since they always have to be across from each other. Once one sits, the other one has no choice where to sit. So since there are 4 couples, each treated as ONE the answer to this question is (4-1)! --> 3!. Or you can draw it like above.
Since the boys are Gentlemen and we, are the ladies we'll be seated first. So the first lady seated is the reference point and she determines how everyone else can be seated. Therefore they'll be (4-1)!. Now you have four spots left for the men to sit. Since the reference point has already been placed the first spot can be used by 4 men, then the next only has 3 men to sit there and so on and so forth. So the men will be 4!. Multiplying those together you'll arrive at 144.
AFTERNOON:
In the afternoon we were lucky to accompanied by Mr. K children Kas and Emilia! (Who by the way, are soo adorable). Anyway, Emilia sat with me and Kas sat with Aichelle. (: Moving along!

Instead of it being 6!, it's (6)(6)(5)(4)(3)(2)(1). This is because if 0(zero) was the first number, it wouldn't be 5 digit numbers anymore, it would only be a 4 digit number. So for the first number, there's only 6 numbers out of the 7 to use. For the second number, no matter what number the first is, there's also 6 options because the zero can be used there now. Then it decreases from there.
The second question is actually not the correct one. This is:

Basically to make it easy you do one set for 0(zero) and another for the other numbers. For 0, no matter what zero has to be the last number which gives you only 1 option. Then for the first number you have 6 other options. Then so on and so forth. For the second part, you have 3 options but no matter which you pick, you only use 1 of them. The first number HAS to be 5 oppose to 6 like the previous because 0 cannot be the first digit otherwise it won't be a 5 digit number anymore. Then you add the two together. (:
Again, that's the wrong answer and the correct one is this:

It's pretty much like the previous part to this question, but instead of 2, 4 and 6, we use 5, based on what the question asks.

This question originally said, How many necklaces can be made from 12 beads of different colours? Thanks to Jojo and his brilliant mind, we realized the actual answer was 1. With 12 beads of different colour, we can make one necklace. It doesn't specify how many different colours. Then Mr. K changed it! But of course, Jojo gets the credit for recognizing it.
To solve this question is fairly straight forward. You have 12 beads, but it's a circle so the first bead is the reference point. So it's (12-1)! Also, since it's a neckalce, if it's flipped it's the same. Therefore you divide by 2 and there's your answer.

This is a Combination type of question. These are when you arrange objects and don't care what order they're in. However, afterwards you DO care what order they're in. So first you just find the different ways that a necklace of 12 beads can be made with 18 beads. (18!/12!6!) Then, for each of those different ways, you need to find out how many different ways the beads can be arranged. So you multiply it by (12-1)!/2. You simplify and come up with your answers.

Since the students have to be right beside each other everytime (consecutive), there's only 6 ways that they can be arranged in the 8 seats (Shown by Aichelle at the bottom of slide). Since there are 4 students, the first seat has 4 students to sit there, then the next 3, the next 2, and the next only 1. So it's 4! multiplied by the 6 different ways they can sit in the 8 seats.

The 3 books that always have to be together, you should just put into a bag until later on in the question (Mr. K's blue bag). Considering the 3 books in the blue bag as 1, the different ways they can be positioned is 6!. Then, if you take the books out, the different ways the 3 books can be arranged is 3!. Multiplying them together you get the answer. (:
Hopefully I explained everything enough for people to understand. I again apologize for the late post. Usually if I have the weekend I like to post it up on that friday. But since things got in the way, it never happened. So again, sorry.
AND.. the next scribe will be the super awesome girl that sits next to me in class, Mel!
Friday, April 20, 2007
Today's Slides: April 20
To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.
Thursday, April 19, 2007
Scribe Post II
We had an unusual start in today's class. When I first came inside the classroom, Mr. K was there, doing his daily morning routine which involves downloading the class' lesson for today. I left to go for a walk. When I came back, Mr. K wasn't there, and when the bell rung, to everyone's surprise, Miss Armstrong and her Grade 10 (Pre-Cal?) class came in. Miss Armstrong was saying that Mr. K is currently in her classroom probably using her computer. She then told us that we were going to do some "math aerobics" and whatnot. Everyone was hesitant at first, but after a while Miss Armstrong got us going and laughing. Richard tried to teach the sine and cosine dance to the Grade 10s and asked everyone to do it, but to no avail. Better luck next time, Richard, haha. ^_^ Mr. K then came in finally, and we started our lesson with the Grade 10s.
We then started off with this problem:

When we did this problem for the first time, we did not include 0 as one of the possible even numbers for the 3rd problem in the slide. I was wondering at first as to why 0 wasn't included as an even number. That got Mr. K into thinking and we tried to find out whether 0 is an even number. After a couple of minutes, we found out that 0 is an even number and therefore was included as one of the possible even numbers, making us change our solutions and answers.
The solution should go like this:
1.1.5.4.5.1.5 = 500 phone numbers
We were then introduced to Permutations:

This is pretty much straightforward. We were then introduced to the next problem:

This problem was solved by one of the Grade 10s (his name is Daniel, thanks Aichelle) that were currently in our class. He figured out that since there were 9 players on the softball team, there could be 9.8.7.6.5.4.3.2.1 or 9! possible batting orders. The first member would have 9 choices when he would bat, leaving the second member 8 choices when to bat. The second member could then choose when he would bat, leaving the 3rd member 7 choices when to bat, so on and so forth. Daniel received a big compliment from Mr. K, who was impressed by the guy's thinking.
On to the next problem:

This problem got most of us back into thinking, but it's actually quite simple. We could use the Fundamental Principle of Counting, or the Pick Formula. There are 120 rooms in a hotel, and guests have reservations for 66 different rooms. The first guest would have 120 rooms to choose from. After he chooses, the second guest has 119 rooms to choose from, 1 less than the first guest because, well, the first guest has chosen 1 room out of the 120 rooms available, leaving 119 rooms for the second guest to choose from. After the second guest chooses a room, the third guest chooses a room out of 118 rooms, then the fourth guest chooses a room out of 117 rooms, so on and so forth. There are at least 2.63x1012 ways the rooms can be assigned to guests.
Using the Pick Formula, nPr = n!/(n-r)!, we just plug in the numbers, as illustrated in the image.
n = 120 rooms
r = 6 guests
We would also arrive at the same answer. I actually prefer using the Fundamental Principle of Counting as it requires you to really think about it first and you would understand the concept more.
(note: Ms Armstrong came after we solved this problem and picked up the Grade 10s. The classroom felt empty after they left, haha.)
Then, the next problem Mr. K gave us got us into thinking. The word BOOK has four letters. How many "words" could we write using the letters from the word BOOK? Hmmm.. Grey-M said that there are 6 possible "words" that could be formed using the letters from the word BOOK. His reasoning is that since there are 2 letter O's in the word BOOK, some "words" would repeat. Mr. K then told us to actually see how many "words" we could come up using the letters from the word BOOK. Most, or all of us actually came up with 12 "words". Mr. K then explains us why in this slide.

Why 12? Well, first of all there are four letters in the word BOOK, giving us 4! different "words" that can be made from that word. But, since there are 2 same letters, we divide 4! by 2! (Actually, I don't actually know yet as to why we divide by the 2! if there are 2 same letters , although I understand the concept. I just can't put into words yet. I'll explain further later when I could, haha.), therefore giving us 12 "words". Mr. K then gave us another example, this time he asked as to find how many "words" can be formed from the letters of MISSISSIPPI. Well:

That was pretty much our lesson for today. I'm just covering for Sandy who couldn't do the scribe responsibilities today, so she'll be the scribe for tomorrow. Homework for today is Exercise 29.




