Exponential Modelling

Hi everyone! Today we talked about exponential modelling and its application into our daily lives. Exponential modelling can be used for carbon dating, population growth and compounding interest. There are two cases to this kinds of problems:
CASE 1
In this case we are only given little information and create our own model of the function.

• This is how the basic function looks like.
• This is the formula that we use when we are only given little information and we have to find the model ourselves.

An example of this case can be seen here:

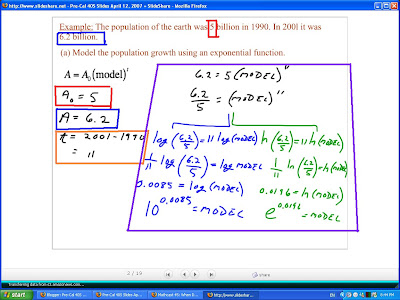
• It is the value that we started off with or the A[naught]
• It is the amount that we end up with after the period or the A
• It is the amount of time that passed or the delta T
• We could find the model by either using a base of 10 or a base of "e". The base "e" is preferrable, because you can get the rate of growth easily b=y just looking at the exponent of "e".

Another way to solve this problem can be seen here:

• 
  
• 
  • 
    
• The only thing that is stopping us to solve get the model is that it is raised to the power of 11Th so we just have to raise both sides to the power of 1/11th to get the same answer to get rid of the exponent.

Part B of the same problem:

• 
  

• 
  • 
    
  • 
    
• In this kind of problem we just need to change the value of "t" and punch it in on our calculator.

We are also reintroduce to the compound interest formula.

• 
  • 
    
  • 
    
• The only difference between this compound interest formulas is that the blue one is used if the interest is compounding continuouslyor there is an infinite amount of compounding.
  

CASE 2

• 
  

• 
  

• 
  

In this case we are given a lot of information because we have the model, period and the A[naught]

• In this case when we are given the model we have to use the formula above.

An example of this case can be seen here:

• 
  • 
    
• This is a straight ahead kind of question because its as easy as just substituting the values and punching it in on our calculators.
  
• 
  

• Another example can be seen here:
  • 
    
• The 50 was derived from the hlaf of the the original substance which is 100 since we are looking for the half life.
  
• In this step we had to use logarithms because we are looking for an unknown value in the exponent.
• 

• This is a straight ahead question because all you need to do is substitute in the values.

During the afternoon all we did was apply all the ideas that we learned in the morning to different kinds of other questions. All this questions can be seen on today's slide.

Thats it for my scribe today. The next scribe is Dino.