Scribe

Hey it's Bertman and it looks like I'm todays scribe.

We started the morning gonig to the gym for the M.A.D.D multimedia presentation. Driving under the influence is a serious offense that dangers yourself and everyone around. Driving high goes the same way, so don't do it!

Anyways we started the afternoon class by watching a youtube video created a by Mr. Greene. The video shows him teach and show everything and anything about our unit, sequences in a matter of 3-4 minutes. Amazing isn't it?

Heres the link : http://youtube.com/watch?v=WjLSz-nNLBc


Following thw questions from the slide, the sum of the intergers 1-5000 can be found by using Gauss' formula. Where "n" = 5000, "t1" = 1 and "d" = 1. Simplifying we get a huge number, 12 502 500.

To find the sum of the numbers from 1-5000 that are multiples of 7, you start by dividing 5000 by 7 to get a value. Which is 714 different numbers. Using Gauss' formula again, "n" is now 714, "t1" = 7 and "d" = 7. Simplifying we get an answer of 1 786 785.

To find the sum of the intergers between 1-5000 excluding the numbers that aren't multiples of 7 can be found by just subtracting the 2 answers previously solved. Mr. K also told us we would be normally given this question and not the first 2.

Now we get to the super-bouncy ball questions!

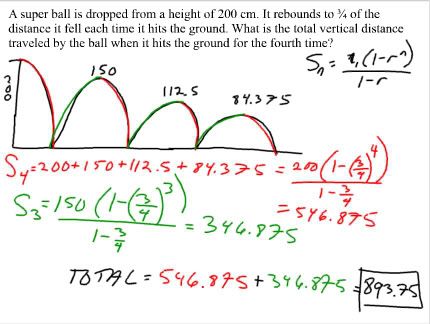
There are 2 distances the ball creates. Distances bouncing up, and dropping down.
The distance of the ball when it's going down decreases by 1/4.
The distance of the ball when it's going up decreases by 1/4

By using the geometric formula, when it's going down, "t1" = 200, "r" = 3/4 and "n" = 4 since we want to find the distances after it hits the ground for the 4th time. When it's going up, "t1" = 150, "r" = 3/4 amd "n" = 3. By adding both numbers we get a total of 893.75.


There is another way to solve this type of question. When using 150 as "t1" the total distance from that first initial bounce to the second is 300. Therefore "t1" can be 300. The other values are the same and you get 693.75 as an answer. Don't forget the add the distances you left out depending on where you started. By adding 200 we get the answer again of 893.75.

Everything else are on the slides, from the sum of inifinity formula and the relationship from the value "r" to the words convergence and divergence. I don't know if we're supposed to pick scribes now that all the units are over but I choose Albert M.

Today's Slides: May 31

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

Here's the movie from the first slide.

Yesterday's Slides: May 30

The internet was down at the end of the day yesterday. Here are the slides ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

Sequence Sequel v.02

Hey guys! This is Jann, and I'll be your scribe for today! =D

We started of our lecture with some "quickies"...

1. Find the value(s) of "r" in 5r^4 = 80

Solution:

In order to solve this question, we just use algebraic methods...
2. In the geometric sequence, if t1 = 3 and r = 2, find t3.

Solution:

If we can recall the rule for geometric sequences from last class...3. If the first term of a geometric progression is 1/3 and the common ratio is -3, find the next 3 terms.

Solution:

In order to solve this, we can simply use the geometric sequence rule to find t2, t3, and t4...

4. Determine the common ratio for the geometric sequence; 1/(x^1/2), 1, (x^1/2).

Solution:

In order to solve this problem, first we pick either the first, second, or third term. We can concentrate on that term to find the common ratio, "r". There is one catch, if we let n = 1, our common ratio will be 1 since "n-1" is the exponent of the ratio. If we use n = 1, then the exponent will be 0, meaning, r will equal 1 (anything to the power of 0 is 1)...

I'll pick the 2nd term...Then, Mr. K told us the story of the great Johann Carl Friedrich Gauss

So, I'll try to tell the story.. XD

One day, Gauss' teacher asked his students to "find the sum of the numbers from 1 to 100". During his time, there were no papers to write on, just slates. His classmates started to add up all the numbers, starting 1. (Man... this is gonna take forever...) Gauss didn't touch his slate and thought about it for approximately 1.5 to 2 mins. He wrote the number 5050 on his slate and handed it in to his teacher. (Even the teacher doesn't know the answer to this one...)

The big question was... "How in the world did he do that?!"

This is how he did it...

1 + 2 + 3 + 4 .... 97 + 98 + 99 + 100
100 + 99 + 98 + 97.... 4 + 3 + 2 + 1

101 101 101 101 .... 101 101 101 101

If we add 2 copies of the sequence, in which one is written in reverse order, we could see a pattern...

Then, Gauss simply put together these numbers...It means that the number 101 has been obtained 100 times in his method. He figured that this answer has been added twice. Therefore, he multiplied the answer by 1/2.

In other words...

t	+	(t + d)	+	(t + 2d)	+ ... +	(t + nd)
(t + (n-1)d)	+	(t + (n-2)d)	+	(t + (n-3)d)	+ ... +	t

(2x + (n-1)d)

+

(2x + (n-1)d)

+

(2x + (n-1)d)

+ ... +

(2x + (n-1)d)

Since 2t + nd = t + (t + nd) = t₀ + t_n,

For any arithmetic sequence, the series could be found by using the Arithmetic Summation...

x+ (x + d) + (x + 2d) + ... + (x + nd) = (n + 1)(a₀ + a_n)/2
or

Where:

"Sn" is the sum of all the numbers up to the "nth" term
" n " is the rank of the nth term
" t1" is the first term in the sequence
" d " is the common difference

A series is the sum of numbers in a sequence to a particular term in a sequence.

For a geometric sequence...

Sn = t1 ( 1 - r^n)/(1 - r)

Where:

"t1" is the first term
"r" is the common ratio
"n" is the rank of the term

Finally, we talked about the "Sigma Notation". It's a short-hand way of writing a series.
The "funky" looking "E" is a Greek letter for "sum". The number above the "E" means "to find the value of n, until we have obtained the nth term of the sequence. "n-1" means that this is the initial value of the sequence; meaning, you have to start evaluating at n-1. "2n - 1" is the "rule" of the given sequence.

That's what we did for this class. (Finally, I have edited my scribe post! Yay!)

Oh well, good night everyone! I'm tired...

Next scribe will be... once again... "BERTMAN" XD.

Scribe - Introduction to Sequences

Hello to everyone once again. Today I am scribing on both the morning class and the afternoon class. In the morning class we had a test on probability so there isn’t much I can talk about there. That’s it for the morning class. For the afternoon class, we started a new unit called sequences. Before we jumped into the work, Mr. K talked to us about fractal and showed us a video on it from www.youtube.com. If you would like to take a look at it, you can look to Mr. K’s post. After that we started off by taking a look at some problems:

Find the next 3 numbers in each sequence of numbers.

4, 7, 10, 13, , , … Answer: 4, 7, 10, 13, 16, 19, 22…

3, 6, 12, 24, , , … Answer: 3, 6, 12, 24, 48, 96, 192…

32, 16, 8, 4, , , … Answer: 32, 16, 8, 4, 2, 1, 0.5…

1, 1, 2, 3, 5, 8, 13, , , … Answer: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

From each of these sequences, we can find out if they are geometric, arithmetic, or neither. Also if it is geometric, then we can find the common ratio and if it is arithmetic, then we can find the common difference. Here are some definitions to help you out:

Sequence: An ordered list of numbers that follow a certain pattern (or rule).

Arithmetic Sequence :(i) Recursive Definition: An ordered list of numbers generated by continuously adding a value (the common difference) to a given first term.
(ii) Implicit Definition: An ordered list of numbers where each number in the list is generated by a linear equation.

Common Difference (d):(i) The number that is repeatedly added to successive terms in an arithmetic sequence. (ii) From the implicit definition, d is the slope of the linear equation.

Geometic Sequence: (i) Recursive Definition: An ordered list of numbers generated by continuously multiplying a value (the common ratio) with a given first term.
(ii) Implicit Definition: An ordered list of numbers where each number in the list is generated by an exponential equation.

Common Ratio (r): (i) The number that is repeatedly multiplied to successive terms in a geometic sequence. (ii) From the implicit definition, r is the base of the exponential function.

Well that’s it for today and that just about covers everything that we went over today in class. Hopefully this helps you guys out a little bit more.

The next scribe is…Bertman!

Homework is exercise 45!

Today's Slides: May 29

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

We lost today's audio. There was a problem with the mic at the start of class. I thought it had been fixed. It wasn't.

Here is the movie we watched and another like it illustrating some of the things I was telling you about:

proBOBly should have done this sooner....

Haha morning of the the test! Not the best time to bob... Well this unit I'm feeling fairly confident in considering the amount of effort I have put into the homework in the exercises and on the blog. A couple of the questions are still worded trickely so I'm fairly certain that a 100% won't happen as I seem to go too fast and miss simple things in the questions on tests. So my goal for this test would be to take it slow and meticulously..... and still finish on time.

BOB IIIIIII

Hello once again, back for my seventh BOB. Well what can I say this unit was a little hard towards the end of the unit, because of the permutations and counting sections which were mixed together. Although I am a little uneasy about those types of questions i believe this test should not be that bad after all. Probability was simply just a concept you had to learn and once you had the hang of it you can challenge any problem you liked. This is why I believe the test should not be difficult, unless there are many counting questions, which I bet there are. So all in all i found this unit to be quite straight forward and not very difficult once the concept is learnt. Good luck to all and make sure to study hard, Probability Test tomorrow morning.

ProBOBility

Hello. It's me again with my bob. So I think that this unit is a pretty straightforward unit. The situations and concepts are easy to understand and the content in the exercises is pretty straight forward. The only problem that I have is that the tricky questions that Mr. K gives us that throws us off. Hahaha. Very Tricky. But at least I get the unit. Haha. So Hope for the best, and everyone do good on the test. Good luck, so long, have fun studying. Cause I am. Haha.

SECOND LAST BLOG?!

Sorry I just posted now. I had work and i just got off. Anyways....Probability what can I say? Its true its the easiest unit but its hard to write down on the paper because there's so many ways you can do it and its hard to decide which one is right. I didn't really like probability ever since junior high well ever since I knew what it was. But whenever we work on problems in class I start to like it more and actually get it. Hmm ... well this is long enough. I'll leave it as it is and study!

GOODLUCK EVERYONE ON THE TEST TOMORROW!

Blogging on Blobbing

Well, this unit about probability started off as relatively easy....then it became a lot harder. The quizzes were sort of a wake up call to me that i need to study more and finish this year strong. I really need to study more on this unit because ever since junior high i struggle on probability. I wish all the best to everyone. Good luck on the test and hopefully we all do well!

Probability Pre-Test

Hello, i am the class scribe for this evening. We started today's class with a pre-test, because tomorrow is our long awaited test on probability. Basically the Pre-test had lasted almost the full class, because many of the students had questions about the questions on the pre-test. So to not get carried away here are the questions and the solutions to the pre-test questions.

question #1: Twelve people including you are members of the choir. The choir director is going to choose three members to attend a workshop. The probability you and two other members will be chosen is:
a. 1/4 b. 3/10 c. 1/12 d. 1/10

The answer is 1/4, because you are going so it is 1 * 11c2, because there are 11 members left and the director needs to pick two of them. It is all over 12c3, because it is over all the possibilities. So once that is calculated it is 1/4.

question #2: Rex is playing a guessing game. The probability he will guess each question correct is 0.3. What is the probability he will guess exactly 5 out of 10 questions correctly?
a. 0.15 b. 0.10 c. 0.29 d. 0.80

The answer is 0.10, because he must get 5 out of 10 questions correct so it is RRRRRWWWWW.
So it is 10!/5!*5!, because there are 5w's and 5r's. Then the 10!/5!*5! is multiplied by (0.3)^5*(0.7)^5 which is the binomial theorem. So once it is all worked out you achieve the answer of 0.10.

question#3: You choose 4 digits from the numbers (0-9), with no repeated digits. To win a prize only two numbers need to match the four selected by the computer.The probability, correct to the nearest one hundredth that you will win a prize.

The answer is 54.76%, because you must take the amount of numbers you are able to match with the computer to win a prize in this case 4c2, 4c3, or 4c4 numbers and divide them over all the possibilities which is 10c4, and add them all up. Once added and reduced it should give you a fraction:23/42, which is 54.76%.

question#4: The serial number of a $10 bill contains 8 digits. If your $10 bill contains the digit 7 at least once, you win a prize. What is the probability that your $10 bill will win?

The answer is you must find the probability of when there are no 7's and then you take the complement. So no 7's is basically 9 out of the possible 10 numbers to the exponent (^) of 8, because there is 8 digits. It gives you an answer of 0.4305, so to get the probability that there is a 7 you must take the complement, so 1 - 0.4305 = 56.95%. which is the answer.

question#5: Jeff takes a lunch to school on two days, and on the other three days he buys it. If he takes lunch he is late for his fourth period class 15% of the time, but if he buys it, he is late 35% of the time.

A) what is the probability that Jeff arrives on time?

The answer is that we take percentages of the two times he arrives and add them together to form the answer. So P(o) = P(to) + P(bo) = (0.4)(0.85) + (0.6)(0.65) = 73% which is the answer.

B) If Jeff was late, what is the probability that he took his lunch to school?

The answer is that you must take the probability he was late and took his lunch to school divided by the time he was late and brought his lunch plus the time he was late and bought his lunch. (0.4)(0.15)/(0.4)(0.15) + (0.6)(0.35) = 2/9 or 22.22% which is the answer.

So he is all of what we had done in class to day, when viewing this scribe post make sure to check the slides if you are confused, because it may help you find the way I had shown the answer. Make sure to study because tommorow is our Probability Test.


Tommorow's scribe is Robert P.

Ohh my BOB

Chello everyone. Another unit has come to a close, like most of you have already said, and I think probability can be the easiest thing to comprehend yet the hardest thing to write on paper. Don;t you hate that, knowing exactly how to solve problems in your head, but don't know how to write it? Or maybe that's just me... Anyways, I'll wrap this up since I should study. Funny how remembering to do this also remembered me to study. Ohh my lanta.

BOB

Another unit done and I'm starting to see a trend. As we start the unit, the concepts and questions seem to be quite easy to grasp for everyone, especially with this Probability unit. However, once the pre-test approaches most of us (from the classes reaction, correct me if I'm wrong) seem to be surprised at the complexity of some of the questions. Whatever it may be, the only way we can possibly improve upon that is study, study and study. Exams are coming very soon and we only have one unit left. Let's finish this year off strong. Good luck on the test tomorrow everyone.

BOB # 7

Hello to everyone yet again. Wow probability has come and gone and the test is tomorrow. This unit started off pretty easy and then it just got harder. On today's pre-test I found question 3 really difficult. To get through this though I will study tonight and try to do well on the test tomorrow. I wish the best of luck to everyone! See yah tomorrow!

bee oh bee number seven.

hello. the end of the unit has come once again and here I am bobbing...probability...I never really liked this unit at all due to the fact that it is challenging...haha I found it challenging ever since junior high. I was able to understand the things we did in class, well most of it. Quiz number one was quite surprising because it showed me what I knew or didn't. Then quiz number two I did a little better, which is good. This unit was difficult for me because I don't realize what is right in front of my face. Hopefully though, on the test I will be able to figure out what is in front of me. Good luck to everyone and hopefully we all do well.

BoB

Well to start off this unit was simple...It seemed like a piece of cake, but right now that point of view that I have just changed... This unit is really difficult, it requires a lot more thinking than I thought it would. The way the questions are worded and the solutions that seem to be the exact opposite of what you do... It's either you over think or under think how to answer the question...

Well the test is tomorrow and I am NOT looking forward to it. I don't feel that I'm ready for it. But there's nothing I can do about it... :P... Oh well I'll just say good luck to everyone... :P

BOB

Hello everyone! Once again, we have finished another unit of our course. Probability has been a very interesting unit because it practices your thinking skills. For me, figuring out chances on how a certain thing will occur is pretty cool. I found the "Tree Diagram" very interesting because it shows you the sample spaces of a certain event.

I hope everyone will do well on this test. This is our 2nd last chance to improve our test marks... -_-

Good luck y'all!! XD

Today's Slides: May 28

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

Probability

Friday is grueling days ever because of 2 unexpected quizzes from Mr.K

First we started-off with this. The very first thing to do is to make a tree diagram and fill out the probability for each cases .The probability that Tony will move to Winnipeg is 2/9, and the probability he will marry Angelina if he moves to Winnipeg is 9/20, all you need to do is to multiply to the probability that Tony will move to Winnipeg and marry Angelina.To get this, all you need to do is to multiply the probability that he is moving to Winnipeg which is 2/9 and the probability that he is not marrying Angelina 11/20.
To get this multiply the probability that he is staying which is 7/9 and the probability that he is not marrying Angelina which is 19/20.This is the probability of drawing four aces in a standard deck of fifty-two cards.
This is the probability of drawing diamond cards.
This is the probability of drawing an ace and a diamond.
All you need to do is to add the probability of drawing four aces and diamond cards, then subtract the probability of drawing an ace and a diamond.To answer this question, you need to make a Venn Diagram. Then from that diagram you will see that ten out of twenty-five students doesn't like either Dr.Pepper or Diet Dr.Pepper.

This is the probability of choosing two green dresses out of six.
This is the probability of choosing four dresses out of nine.
This is the probability of choosing six dresses out of fifteen.
All you need to do is just by dividing the favourable cases over the possible outcomes.

First thing is to make a tree diagram and fill out the probability for each cases. Next is to get the probability of an SUV that has air conditioning and divide it by the probability of having a passenger car that has air conditioning plus the probability of an SUV that has air conditioning.

To get this, just add the probability of drawing a defective blade first and then a good blade and the probability of drawing a good blade first and then a defective blade.
For the 1st question, you can't use the number 0 as the first digit, so you nine choices left.
The 2nd digit, you can't pick the same number that you use before so you have nine choices left. The 3rd digit , you can't pick the same number that you use for the 1st and 2nd digit, so you have 8 choices left. The 4th digit, you can't pick the same number that you use from the previous three, so you have 7 choices left.

For the 2nd question, just divide the possibility of having an odd number by the total number of possible digits.

For the 3rd question, break the question into 2 steps,one is that ending in zero and the other is ending in 5, then add both . Then divide the answer by the total number of the possible digits.

To get this, get the probability of getting exactly four hits out of 6 throws. Then, raise the probability of hitting to the fourth power and then the probability of missing to the second power.

That's it folks.By the way we have a pre-test tomorrow,sorry for the late scribe .The next scribe is DINO.

BOB-ing 7

I'll go straight to the point. The Probability Unit evokes chaos in my mind. In short, probability is one of those units in Math that makes me go, "WHAAAT?!" It may not seem like it because I don't do it in class. But seriously, in my head, I do it a lot. I grasped the concept easily. However, the application of that concept is the real puzzle to deal with. Maybe, the struggle originates from lack of practice and absence of confidence with myself. Like in the last quiz, I doubted myself so much that I erased the solutions for two questions that transpired to be correct. That was really... KJ (kill joy). Another frustration dawned upon me as the week concluded and the weekend commenced. I promised that I would be practicing during the weekend, but I failed to such a thing. Some problems throw me off because of too many disturbances. I really hope that I do well in this test, but not without a lot of practices. Maybe I should start after this BOB! Anyway, this year is about to end and I couldn't ask for more with a fun class already at hand. But, it's so fun that sometimes my attention linger over other topics. My BOB ends here and I hope you all had a great weekend and good luck on the upcoming pretest and test! See you guys tomorrow!

I hope that all my practices will pay off. Good luck guys! I know I need that too! HAHA!

BOB 7

Well, I thought that this probability unit was kinda easy. When we had the quizzes, I was surprised! It was hard, and that led me to think that I needed more practice for this unit. I'm just hoping that the test won't be as quite difficult as the quizzes. Those quizzes really got me surprised. Anyway, I wish everyone luck in the test, we're going to need it.

B O B

Hrm, yet again it's time to blog. This unit went by quite fast. During the beginning of this unit, the problems were without a doubt easy and included no difficulties for me. However, as we progressed, I found that there were questions (such as those on the quiz) that surprised me.

On the otherhand, I should've been more responsible for completing more of my exercises than I have. I found that since I did not practice as much, I struggled at times and found that I was stuck; not knowing what to do next on certain questions.

Truthwise, I will "try" to do more practice questions tonight and we'll see how I fair on the pre-test and test.

Good luck everyone on the pre-test and test this coming week!

BBOOOOO for BOB

So apparently we have a test on Monday ... wasn't in class on Friday unfortunately for the quiz. This unit that people call "probability".. is the story of school life. This is the unit i dread every year. This unit Probability was so difficult, hands down this has to be the hardest unit . I honestly wish we had like an extra week so i can actually take the time to understand this unit a bit more, i know for sure this is going to be my worse unit yet.
But, for everyone else Good Luck because i know you'll all need it just as much as i will.

Boron-Oxygen-Boron

I almost forgot to bob for the upcoming probability test until I checked the blog and saw Sandy's. And to iterate Sandy's statement, the provincial exam is only 2 weeks away! I can't believe that we've blown through the year in almost no time at all (well at least it felt like that) and what a blast it's been. Though I'm feeling really down because of all the cruddy marks I've been getting recently, but I've really enjoyed this course so far. This was the first class which presented a functional lesson solely integrated upon the smartboard. But enough about reflecting over the entire year, this bob's supposed to be about just this unit xD. This unit of course was probability. This unit wasn't terribly difficult and didn't present a lot of tribulations, especially seeing as the final portion of probability incorporated one of our previous lessons: combinatorics. Just remembering that a probability can be found by dividing the amount of favorable outcomes by total amount of outcomes is how you arrive at the wanted probability. Well this unit was very relaxed and somewhat straight forward, but as Mr. K left us (made me sad )= ) we were responsible for our own learning, and showing by my quiz marks, I wasn't exactly a very reliable worker. But as for the rest of the unit, there wasn't really anthing new that was unique to other units except for the exciting colloquy we had with Eddie's class in Georgia! It was quite a surreal experience, seeing as it's quite intriguing to converse with people from other regions of the world. I think we were all excited to chat with the class over in Georgia, and when the day came, we really enjoyed it. I think it was quite an extravagant episode in our bevy of pre-calculus memories. But with that said, I can't wait for further conversations from the class over in Georgia. This was my bob, good night everyone. As for the test:

I WISH EVERYONE GOOD LUCK ON THE PRE-TEST AND TEST!!!

99.9 BOB FM! (8)

Every single time I arrive on our blog I think about how close the provincial exam is. 2 weeks from tomorrow! It's really time to start studying. As for this unit, I didn't do great on my quiz, but the mistakes were really dumb. -_-" As soon as I seen the correct answer I realized I had made a stupid mistake. Regardless of the quizzes, I think this unit is pretty straight forward and not that difficult at all. I hope to do as good on this test as my logs one. (: Hopefully everyone else does really good as well. Good luck to everyone with the up coming test! <3

Today's Slides: May 25

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

The Winnipeg Georgia Connection

I thought you might be interested in this follow up to our gizmo conversation with Mrs. Davis' grade 5 class in Gerogia. I've mirrored the post in it's entirety from her blog. Listen to the various mini-podcasts at the end:

Canada/Georgia Connection on Gizmo
May 22nd, 2007 9:02 am

The blogicians and the students in Darren Kuropatwa’s Pre-Cal 40S class participated in a Gizmo call last week. The blogicians had prepared some questions that they wished to ask the high school students. Gizmo has a neat feature that lets you record the conversation as you are talking. It did pretty well but does have an echo effect from time to time. As I listened to these podcasts I really marvel at the learning that occurs. I kept thinking how much was going on and how much can be fostered with these types of connections. I think you have to have a plan of action as if you just connect and talk you may lose some focus. It was a thirty minute call that was filled with some many unexpected turns that were so worthwhile.

What a good space to give kids practice with public speaking. Both ages were nervous but the experiences they got speaking will serve them so well. I think both sides learned so much from each other. The older students were unaware of some of the constraints involved while teaching elementary students (listen to the chat box podcast), the ability to look for dramatic and outstanding pictures for presentations (listen to the Flickr podcast).

On a scribe post after the Gizmo talk, Grey-M one of the high school students said the following:

I must say that trying to answer something on the spot is brutally hard (These weren’t easy questions either) so people, including me, were a little hesitant at times to respond. So that was a fun deviation from our usual routine.

The younger students are in awe of the older students but in these kind of connections they learn to step back and decide if they agree or not. They learn that that is OK.

Johnny from the blogicians posted the following after the talk:

We just did a gizmo chat and it was quite delightful with a pre call math class and it was nicely spoken by me and my classmates. Mr. K was the teacher of the class I asked about chat box and how they use it and Danny replied “We use it to learn all over the web and it sort of saves time instead of commenting”. I sort of agree with him what do you thing do you agree or do you disagree? If you don’t know what it is try looking it up and using it.

You get to discuss so much and the best part is you are having authentic conversations with the students and encourgaging their honest input. It builds great learning communities. This can only make things better in our classrooms. This is great practice for them and us. The teachers get to do a lot of learning too. We’re learning how to best orchestrate these experiences. We’re learning how to help these kids on their path to becoming global citizens. The more experience we can give the kids with this type of learning the more they will be able to help us shape its’ most effective use. These are the types of literacies we need to be developing in all our schools.
I’m still thinking about all this….. the possibilities, how to involve others, and on and on….

It was a day to remember - a day of connections and learning between some very inspiring students in Canada and Georgia.



Links to podcasts:

Podcast 1: Introduction and special bond

Podcast 2: Eddie Chris Online Safety

Podcast 3: Eddie Vincent Being responsible while blogging

Podcast 4: Emmy Danny Flickr

Podcast 5: MV Chris Craig B.O.B (Blogging on blogging) and convincing middle school teachers to let students blog

Podcast 6: Tina Vincent Grey-M The best and the worst of blogging

Podcast 7: Johnny Richard Danny Chat Boxes

Podcast 8: Eddie Aichelle How does blogging advance your learning as a fifth grade student?

So, when you were writing your scribes and BOBs on Circular Functions did you ever imagine a grade 5 student from Georgia would drop by, read what you wrote, be interested in it? That he would blog about it which would lead to all these ripples in the blogosphere? That all this would eventually connect you all, on a very personal level, with a class of grade 5 students half a continent away?

When you publish your learning online, even if it's tough stuff like math, you have an audience that spans the globe, grades and geography.

Did you ever imagine something like this would happen? ;-)

Probability Practice Produces Perfection ... Probably

As promised here is a little extra probability practice for you ...



And some links for learning ...
Take this quiz on Probabilities of Compound Events.

Take this quiz on Conditional Probability.

Take this quiz on The Binomial Theorem and Probability.

Take this test on Combinatorics and Probability.

Take Harry Potter's quiz on Combinatorics. Try not to run into any walls. ;-)

Try this Probability quiz.

Photo source: Harry Potter's Platform 9 3/4!!!

Exactly why are doctors so cagey?!

Hey it's MrSiwWy here to present to you the scribe post for today! I'm the scribe for today's rather intriguing but yet solemn class. I say solemn as I think that the main question our class was focused around pertained to very serious matter. But anyways, onto the scribe post for
Tuesday, May 22, 2007.

Our class began with Mr. K outright stating to the class that we're on the verge of the end of probability, and the beginning of our final unit: sequences. He then told us that he won't be present the two following days, but that we only have two things left to learn in probability, one of which incorporates one of our earlier units: counting and combinatorics. He presented us with an example of such a question. This question was regarding the arrangement of students, like we have been presented with in the past.
If students are to be seated in 7 desks, what is the probability that Mark and Robert are sitting together?
Basically, we take amount of favorable outcomes, which would be the amount of ways Robert and Mark can be seated together, then divide that by the total amount of seating possibilities.

We quickly moved onto the class for today, and very soon, we transitioned into the question that Mr. K left us off with on Thursday; "Why do doctors have do so many tests? Why are they so cagey?" Once Mr. K put up the question we were to dissect, he set us up in small groups of four. This smoothly yet appropriately forwarded the momentum of our class into the actual lesson. This question can be seen on the following slide:

If we think about each of the four possibilities, we have to realize that the test is to check for cancer, so if it tests positive when the person really does have cancer, then the test succeeded, meaning that it has a probability of 98%, or 0.98. This means the remaining probability (that the test failed by showing negative, when they really have cancer) is 2%, or 0.02.
But as for people who do not have cancer, if the test shows positive, this means that the test failed, and this probability is in fact 2%, or 0.02, and the remaining probability (to test negative for those who do not have cancer) is 98%, or 0.98.
And as I stated at the end of the slide, a tree diagram can really help. So here is a tree diagram that was used to calculate the probabilities of each of the questions on the following slide.

Mr. K later asked us to construct this tree diagram to help us understand the question's calculations, but really, to create one beforehand is more of a help.

Here we see that Mr. K coded certain important aspects for various reasons. These reasons are very vital when contemplating a method to approach each question.
The blue underlined portions indicate that we're dealing with people who have cancer.
The green underlined portions indicate that we're dealing with people who do not have cancer.
The small circular flower symbols indicate total amounts of people that have cancer.
The small stars indicate total amounts of people that have been tested positive for cancer.
The last two are particularly important because the main question that we were originally asked was what the probability of a patient that has cancer is also tested positive for cancer. In order to arrive at this, we must dignify how many total people have cancer, and divide that by the amount of people that were tested positive. We've already learned that in order to find the probability of an event, we take the amount of favorable outcomes and divide that by the total amount of outcomes. So in this case, we take the amount of subjects who have cancer, and divide that by the total amount of times that the test would show a positive result. That is why Mr. K signified each of the above portions. This was taken care of in part 4 of the above questions, but before that, I'd like to outline how to achieve each of the answers in the entire slide.
In order to determine each of the answers shown on this slide, we used the tree diagram above in conjunction with the sample group of 1,000,000 people.

1. This part was simple. Since we know that there are 1,000,000 people, and 0.5% of these people have cancer, that means that 5000 people have cancer, and the rest don't. The rest can be found by subtracting how many that have cancer from the total of people, this gives us 995000.
2. In this part we use the tree diagram to determine what percent of people that have cancer will test positive. To do this we multiplied the amount of people that have cancer, then multiplied that by the probability of testing positive, which is 0.98. This gave us 4900, the answer presented in the slide. For b, since we know 4900 tested positive, the rest of the people who have cancer must have tested negative, and that number is 100.
3. Here we repeated the same process used in part 2, exact that we used different values since we're looking at only the people who do not have cancer. We know that there are 995000 people that do not have cancer, and as I outlined earlier, since the test would fail if it said positive, we would have to find 2% of 995000. This, as shown, is 19900, and to find how many tested negative, we just subtract this from the total. 995000-19900 gives us an answer of 975100.
4. The final part was compounding what we determined in the previous steps, and in essence, determining the answer to our original question. First we take how many people altogether tested positive, we get this simply by adding those that have cancer that tested positive together with those that don't have cancer but tested positive. For b, we know that of the people that tested positive, 4900 of them actually had cancer. So to find the original question at hand, this was the work shown. I already described how this was found, here is the work:
   

As he showed us that vertical line separation between the C and the P, the class began wondering what that represented. This introduced the class to conditional probability. The way Mr. K described such a probability was "when we have inside information" beforehand. Usually when we have dealt with probability we knew that either one thing or another can happen, then another event can happen in one way or another. But in conditional probability, we know that one of these events is going to happen in such a way. In this question, we knew that our answer only concerns when we know that the test is going to be positive. He gave another example of conditional probability using three jars containing marbles. He says that if jar one has 3 blue and 3 red marbles, jar 2 has 2 blue and 3 red, jar 3 has 2 blue and 2 red, then he doesn't look at any of the jars and pulls out a blue marble out of one of them. In this case, we know that the marble that he pulled out is blue. Given the above information, what is the probability that it is from jar 2 of pulling a blue marble from jar 2? This isn't word for word, but I believe that was the basis of the example Mr. K conveyed to us. The basic idea is that we know that the marble is going to be blue, similar to how we knew that the test was to be positive in the first question today. So to sum up conditional probability:
Conditional probability is when we have some inside information on the events at hand, basically when we know some of the information before we even start to calculate.
When we are dealing with conditional probability we write P(P1P2), where P1 is the probability that we're looking for, the vertical line says "given that we already know", and P2 is the event that we already know.

Once we were finished with that question, we moved onto a very similar question, in which he just changed "cancer" to "industrial condition," 98 % to 99 % and 0.5% to 1%. Here is the question along with the work, of which I will of course explain.

Here we see both a tree diagram and the work to the solution for the question.

• I represents those with industrial disease.


• H represents those without industrial disease.


• P represents those that tested positive for the disease.


• N represents those that tested negative for the disease.

Here we see that we found the probability that someone has the disease and also tests positive for the disease by dividing the favourable outcome (probability of having the disease) by the total amount of testing positive. This is exactly the same case as finding the probability of having cancer and testing positive for cancer, just with different probabilities.

So in this class, we fully determined the answer to the question that Mr. K had left us with on Thursday afternoon.

Doctors aren't necessarily cagey, but run the tests more than once to make sure. If we look at the results that we achieved by both questions, we arrive at the fact that if someone really has the disease and tests positive, there's not a good chance that it's for sure. Thus, doctors run tests more than once not for fun or anything of the sort, but in both cases it's more likely or equally likely to be tested positive and not have the disease, so it's good to be sure before breaking such news to a person.

And that concluded our class for today, with the lesson of conditional probability that was presented to us today, as Mr. K said, we don't have a lot left in this unit. This was my scribe post, and I hope it was clear enough for anyone to understand. I still need to fix some content up, really don't like how my Computer is so resilient, especially seeing as I can't get to any pod casts. =/ But as soon as my computer begins to cooperate with me I'll get everything fixed up and tidy. Please just contact me if there are any concerns, questions, complaints, errors, etc. Have a good night everybody!
oh yes, thank you John for reminding me. The scribe for tomorrow will be: Jann!

Today's Slides: May 22

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

LONG Weekend = LONG Scribe

This class was the second one of the unit of PROBABILITY. That is, as Grey-M stated in the last scribe post, the easy unit of PROBABILITY, but anyway...

...The class started with the student elections. 3 of the 4 candidates for the executive council were in our class so it was a fairly bid deal. (To see the results, check the post prior to this one by Sandy.)

After that, we reflected upon the extraordinary video display by Richard in the previous day's candidates' speeches. We liked it so much in fact, that we searched YouTube for it. We didn't find it, so instead we watched a video that was completely irrelevant to math, or anyone in our class for that matter =D.

Then, we got down to some "ACTUAL MATH!"

The first slide shown was a little too easy I believe, but Mr. K. didn't find it as such (haha!)
Then, Mr. K presented us with on that was a little higher on the difficulty scale. We were to "TEST THE QUESTION FOR INDEPENDENCE".
We'll take a quick trip back and review exactly what an independent variable is:

Thank You Grey-M! =)

Now, to test a question such as:

30% of seniors get the flu every year. 50% of seniors get a flu shot each year. 10% of seniors get the flu even though they've had a flu shot. Are getting the flu and getting a flu shot independent events?

•The first step is to look at the set. (In this case it is the SENIORS)
•Next, identify the categories. (Whether they GOT THE FLU SHOT or NOT)
•Now, we identify what event can occur to each category. (they can GET THE FLU or NOT)
• The fourth step in the solving in this problem is to draw a tree diagram:
•Now we can write in the probabilities of each event.
•Then, find the favourbale outcome, or the outcome which we want.
•Now just calculate the probability of the favourable outcome and compare it to the given percentage:
Here we see that the probability of catching the flu and getting a shot is not 10%, it is 15%. This means that they are not independent events.


Next, we moved on to questions that dealt with events that were "MUTUALLY EXCLUSIVE". This means that it is a situation in which one(or more) of the outcomes of the event becomes impossible if the other(s) is(are) chosen.
EXAMPLE:
If Mr. K. were to pick from the class one boy, he will not be a girl. If he picks a girl, she cannot be a boy.
An event can be determined to be mutually exclusive (or "disjoint") if the probability of getting both outcomes is zero(Ø), also known as an empty step.

**both events would be written as "A", "(upside-down U)", "B".**

After that we did problems that asked for the probabilities of "AUB" (A or B). If it is mutually exclusive, then simply add the probability of "A" and the probability of "B".
However, if it is not Mutually Exclusive, we must also subtract the probability of "A and B", because it is not A OR B if both are chosen:

We continued the class by doing more questions dealing with "AND" and "OR" and finished off with a couple situations for which we had to decide whether it was either:
INDEPENDENT or DEPENDENT and MUTUALLY EXCLUSIVE or NOT MUTALLY EXCLUSIVE.
This can be found in the slides (2 posts previous to this one).

To finish off:
•CONGRATS RICHARD AND VINCENT!
•Hope everyone's Long Weekends were better than mine.
•TUESDAY'S SCRIBE IS MR. SIWWY!!!
•Enjoy your day off =D

Congratulations!!

Well.. since our homeroom does contain 3 out of 4 candidates for the school elections this year... I think this blog deserves this post.

Congratulations to Richard who is next years wonderful President!
and... Congratulations to Vincent who is next years wonderful Vice-President!

You guys worked hard and you both deserve your positions on the executive council. I'm definitely looking forward to next year with you two. (:

So again, congratulations to the both of you. =)

Today's Slides: May 17

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

TranSCRIBIN'

Well today we had some different classes....

We started off with a Gizmo call to the Blogical Minds class in the US. Unfortunately I had completely forgot that this was going to happen in the hectic last couple of weeks so I did not have any questions prepared for them. But they had plenty for us :-). I must say that trying to answer something on the spot is brutally hard (These weren't easy questions either) so people, including me, were a little hesitant at times to respond. So that was a fun deviation from our usual routine.

But to the mathematics....

Easy mathematics :-)....

Well we all seemed to grok this probability thing. Today we learned to distinguish between dependent and independent events and how to calculate dependent event probabilities.

A dependent event is an event that the first event effects and and independent event is an event that does not depend on what happens in the first event. So we did a few questions to demonstrate this concept...


The only one event that effects the other event is the removal of the card without replacement because that changes the sample space.

Changes in sample is not the only way to cause dependency. If something within the sample space is changed it changes the odds of the events as shown in the next question.



When a marble is drawn it is replaced with a marble of the other color changing the odds and making this another dependent situation. We got the odds at the end of the probability tree by multiplying along the branches. Then to get a combined probability figure you add all the favorable outcomes.

As we saw with other questions this process generally works for calculating the odds of a singular/series of event(s) . We also found another way this relates to combinatorics in this class because Mr.K showed us that the questions can seem different but they will actually be the same like the flipping of the coin and the children. So this concept seems to be fairly simple but Mr. K will find a way to make this hard on the test. Which I hope will be soon so we can get a few days of review at the end of the year.


Auf Wiedersehen (See if answer tips can get that)

Today's Slides: May 16

Here they are ...





To see a larger image of the slides go here. When you get there you'll see a button in the bottom right-hand corner that says [full]. Click it and the slides will display in full screen mode.

SCRIBE! ( ^.^) Introduction to Probability

Hello fellow classmates and readers! I'm Tim-Math-Y your scribe for today! Today we looked at the beginning of our new unit: Probability. We talked about things such as favourable outcomes over total possible outcomes, certain events, impossible events, sample space and other interesting things.

We started off the class by looking at this interesting question:

• There was no right or wrong answer in this exercise.
• Mr. K was looking to see what we thought of probability and why we chose each numerator or denominator.

While going over each solution that the class came up with, we found that 1/(infinity) is pretty much equal to zero since it comes so close to zero.

• Here we find that 4/9 (0.444 repeating) + 5/9 (0.555 repeating) = 9/9 (1)
• It is quite interesting to see that these two repeating numbers added together gives us the value of 1.
• What we were trying to get to here was the fact that if a number comes so close to another number, we can assume that it takes that form (Ex. 1/infinity = 0)

Next we took a look at the meanings of probability and it's characteristics, including sample space.

• Notice that the "Compound Event" examples are involved in one of our last units, Counting. Specifically, the Fundamentals of Counting.

Next we observe carefully more characteristics of a probability.

• The slides today are quite self explanatory.

Next we looked at some examples of probability.


Next we looked at examples that involved finding the sample spaces.

• To find the sample space of the problem, we find the total possible outcomes either through a tree diagram or a chart/table.
• We are usually only asked this when there aren't a large number of possibilities (will be too much work)

Now we look at more examples:

• To find the probability, we divide the total number of favorable outcomes by the total number of possible outcomes.

Now we look at a really hard example:

• This is one of the attempts of solving question 1a, by one of our fellow students, John

Running out of class time, Mr. K steps in to give us the solution:

• Remember that making mistakes benefits the class in learning*
• Mr. K makes a chart with the times the bus will arrive at the top and the times of the train will arrive on the left.
• Doing this, we find the total number of ordered pairs: also known as the sample space :)

Well that was all for today guys. I know it isn't as flashy and isn't that long or awesomeness to the max but yeah, I was sidetracked a lot today haha.

Well, that wasn't too bad. Most of it was self explanatory.

Tomorrows scribe is... hmmmm...

Grey-M..

Sorry, didn't know who to pick, and it's almost SAMS BDAY HAHAH!