Pre-Cal 40S (Winter '07): ... <-- Ellipse

Once again my scribe post comes late. (This is Ronald McDonald’s fault…) lol… But anyways… Let's start learning about ECLIPSES

We started off the class by figuring out if the two questions below are circles or ellipses…

x² + y² – 10x +4y + 20 = 0
x² + y² + 6x - 2y + 12 = 0

But before that let’s do a little recall from the past lessons from a couple of days ago…

h = x- coordinate for the circle’ center
k = y – coordinate for the circle’s center
r = radius of the circle

Equation of a Circle:

(x – h)² + (y – k)² = r²

Equation of a Horizontal Ellipse:

Equation of a Vertical Ellipse

“a” would always be the higher denominator, which leaves the other one which is then named
“b”.

“a²” defines an ellipse as horizontal or vertical.

If “a²” is below the “x - value” then it is a

horizontal ellipse, then if it’s below the “y - value” then it is a vertical ellipse.

Now Back to the Scribe post I go…

x² + y² – 10x +4y + 20 = 0

First we group the X- Values and Y-Values, then give them homes (parentheses).

(x²– 10x) + (y² +4y) + 20 = 0

Then we prepare to complete the square so we subtract 20 from other side of the equation.

(x²– 10x) + (y² +4y) = - 20

Now we can complete the square…

RECALL:

Completing Squares…

You take the Coefficient of “x”, divide it by 2 and then square it. The answer is then added to both sides of the equation

SO…

(x²– 10x + 25) + (y² + 4y + 4) = - 20 + 25 + 4

Factoring out the given we get…

(x – 5) ² + (y + 2) ² = 9 -------- (x – h)² + (y – k)² = r²

From the simplified form of x² + y² – 10x +4y + 20 = 0 we can now derive the circle’s CENTER and RADIUS…

CENTER (h, k) = (5 , -2) RADIUS = 3

THEREFORE x2 + y2 – 10x +4y + 20 = 0 IS A CIRCLE

**************************************************

Similarly, we do the same steps for this equation…

x² + y² + 6x - 2y + 12 = 0

(x² + 6x) + (y² - 2y) + 12 = 0

(x² + 6x) + (y² - 2y) = - 12

(x² + 6x + 9) + (y² - 2y + 1) = - 12 + 9 + 1

(x + 3) ² + (y - 1) ² = -2 -------- (x – h)² + (y – k)² = r2

From the simplified form of x² + y² + 6x - 2y + 12 = 0 we can now derive the circle’s CENTER and RADIUS…

CENTER (h, k) = (-3 , 1)

RADIUS = -2 or 2i (Imaginary)

A CIRCLE CANNOT HAVE A NEGATIVE RADIUS SO THIS MUST NOT BE A CIRCLE… WHICH MEANS IT'S AN ELLIPSE...

THE ANATOMY OF AN ELLIPSE

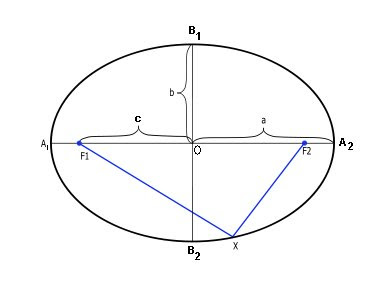
O: The center of the circle

A: Vertices or The End Points of the Major Axis

They are “a” units away from the center of the ellipse

2a = Length of the Major Axis

B: End Points of the Minor axis

They are “b” units away from the center of the ellipse

2b = Length of the Minor Axis

F: FOCUS (Plural: Foci)

They are “c” units away from the center of the ellipse

The Blue Line is called the Focal

Radii. The sum is equal to the Major Axis or

“2a”

READING THE STANDARD FORM OF AN ELLIPSE

For a Horizontal Ellipse...

For Vertical Ellipses...

SOLVING FOR THE EQUATION OF AN ELLIPSE

**Find the Coordinates of the Foci...

**Find the Coordinates of the Vertices...

**Find the Length of the Major and Minor Arcs...

x² + 36y² = 36

One side of the equation has to be be equal to 1. The only way to make one side equal one is to divide 36 by itself.

(x² / 36)+ (36y² / 36)= 36 / 36

Dividing both sides by 36 you get...

(x² / 36) + y² = 1

So far we are able to determine the center of the ellipse... which is (0 , 0) since there is no values for "h" and for "k".

Now you can use the formula for the ellipse to get the variables needed to get the values of a, b & c. But first we have to figure out if the ellipse is horizontal or vertical. How? By looking for the denominator with the highest value or "a²". Since "y" ' s denominator is 1 and "x" ' s denominator is 36, a² must be equal to 36, meaning that the ellipse is horizontal.

You can now use the formula for a Horizontal Ellipse to get the values of "a", "b" and "c"

a = 6 , b = 1

Remember that the Major Axis is equal to 2a, and the Minor Axis is equal to 2b...

Major Axis is 12

Minor Axis is 2

This triangle comes from the Semi- Major Axis, Semi- Minor Axis and Focal Radius.

Now that the values of "a" and "b" have been found, we can use the Pythagorean Property to find the value of "c"

c² = a² - b²