Hey it's Bertman and it looks like I'm todays scribe.
We started the morning gonig to the gym for the M.A.D.D multimedia presentation. Driving under the influence is a serious offense that dangers yourself and everyone around. Driving high goes the same way, so don't do it!
Anyways we started the afternoon class by watching a youtube video created a by Mr. Greene. The video shows him teach and show everything and anything about our unit, sequences in a matter of 3-4 minutes. Amazing isn't it?
Heres the link : http://youtube.com/watch?v=WjLSz-nNLBc
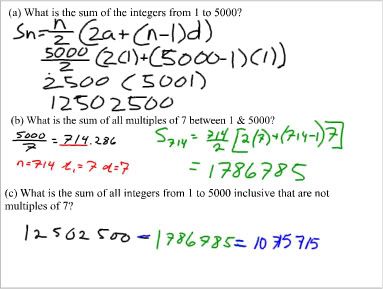
Following thw questions from the slide, the sum of the intergers 1-5000 can be found by using Gauss' formula. Where "n" = 5000, "t1" = 1 and "d" = 1. Simplifying we get a huge number, 12 502 500.
To find the sum of the numbers from 1-5000 that are multiples of 7, you start by dividing 5000 by 7 to get a value. Which is 714 different numbers. Using Gauss' formula again, "n" is now 714, "t1" = 7 and "d" = 7. Simplifying we get an answer of 1 786 785.
To find the sum of the intergers between 1-5000 excluding the numbers that aren't multiples of 7 can be found by just subtracting the 2 answers previously solved. Mr. K also told us we would be normally given this question and not the first 2.
Now we get to the super-bouncy ball questions!
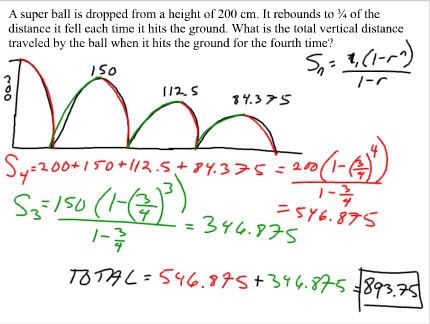
There are 2 distances the ball creates. Distances bouncing up, and dropping down.
The distance of the ball when it's going down decreases by 1/4.
The distance of the ball when it's going up decreases by 1/4
We started the morning gonig to the gym for the M.A.D.D multimedia presentation. Driving under the influence is a serious offense that dangers yourself and everyone around. Driving high goes the same way, so don't do it!
Anyways we started the afternoon class by watching a youtube video created a by Mr. Greene. The video shows him teach and show everything and anything about our unit, sequences in a matter of 3-4 minutes. Amazing isn't it?
Heres the link : http://youtube.com/watch?v=WjLSz-nNLBc
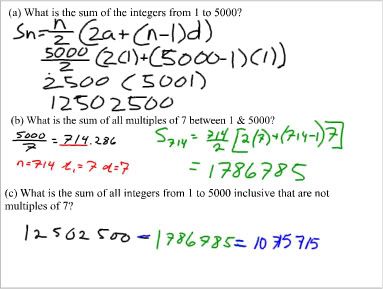
Following thw questions from the slide, the sum of the intergers 1-5000 can be found by using Gauss' formula. Where "n" = 5000, "t1" = 1 and "d" = 1. Simplifying we get a huge number, 12 502 500.
To find the sum of the numbers from 1-5000 that are multiples of 7, you start by dividing 5000 by 7 to get a value. Which is 714 different numbers. Using Gauss' formula again, "n" is now 714, "t1" = 7 and "d" = 7. Simplifying we get an answer of 1 786 785.
To find the sum of the intergers between 1-5000 excluding the numbers that aren't multiples of 7 can be found by just subtracting the 2 answers previously solved. Mr. K also told us we would be normally given this question and not the first 2.
Now we get to the super-bouncy ball questions!

There are 2 distances the ball creates. Distances bouncing up, and dropping down.
The distance of the ball when it's going down decreases by 1/4.
The distance of the ball when it's going up decreases by 1/4
By using the geometric formula, when it's going down, "t1" = 200, "r" = 3/4 and "n" = 4 since we want to find the distances after it hits the ground for the 4th time. When it's going up, "t1" = 150, "r" = 3/4 amd "n" = 3. By adding both numbers we get a total of 893.75.

There is another way to solve this type of question. When using 150 as "t1" the total distance from that first initial bounce to the second is 300. Therefore "t1" can be 300. The other values are the same and you get 693.75 as an answer. Don't forget the add the distances you left out depending on where you started. By adding 200 we get the answer again of 893.75.
Everything else are on the slides, from the sum of inifinity formula and the relationship from the value "r" to the words convergence and divergence. I don't know if we're supposed to pick scribes now that all the units are over but I choose Albert M.

No comments:
Post a Comment