You can take a sneak peak at the new blog here.
Click that picture ... there's a great article at the other end of that link.
Expanding the walls of our classroom. This is an interactive learning ecology for students and parents in my Pre-Cal Math 40S class. This ongoing dialogue is as rich as YOU make it. Visit often and post your comments freely.

 Mr. K then showed us what an exponential function was. F(x) to the exponent 2x. For example,
Mr. K then showed us what an exponential function was. F(x) to the exponent 2x. For example,  He then explained to us that :
He then explained to us that : 

 It is read: Log base b of c is a or log of b c is a. We then went over a review of changing the graph. x+2 shifts the graph 2 units to the left, -(x) causes a vertical flip, and (-x) causes a horizontal flip. To end the morning class Mr. K pointed out that the point (0,1) will always be present on the exponential function graphs and that the point (1,0) will always be present on the logarithm graphs.
It is read: Log base b of c is a or log of b c is a. We then went over a review of changing the graph. x+2 shifts the graph 2 units to the left, -(x) causes a vertical flip, and (-x) causes a horizontal flip. To end the morning class Mr. K pointed out that the point (0,1) will always be present on the exponential function graphs and that the point (1,0) will always be present on the logarithm graphs. The teaching of mathematical concepts is the main focus of this project; so we can teach other people and learn at the same time.
Acheivement Descriptors
Instead of levels 1-4 (lowest to highest) we use these descriptors. They better describe what this project is all about.
Novice: a person who is new to the circumstances, work, etc., in which he or she is placed; a beginner.
Apprentice: to bind to or place with a master craftsman, or the like, for instruction in a trade.
Journeyperson: any experienced, competent but routine worker or performer.
Expert: possessing special skill or knowledge; trained by practice; skillful or skilled.
| Acheivement | Mathematical Challenge (25%) | Solutions (55%) | Presentation (20%) |
| Novice | Problems illustrate only an introductory knowledge of the subject. They may be unsolvable or the solutions to the problems are obvious and/or easy to find. They do not demonstrate mastery of the subject matter. | One or more solutions contain several errors with insufficient detail to understand what's going on. Explanation does not "flow," may not be in sequential order and does not adequately explain the problem(s). May also have improper mathematical notation. | Presentation may or may not include visual or other digital enhancements. Overall, a rather uninspired presentation. Doesn't really stand out. It is clear that the student has invested little effort into planning their presentation. |
| Apprentice | Problems are routine, requiring only modest effort or knowledge. The scope of the problems does not demonstrate the breadth of knowledge the student should have acquired at this stage of their learning. | One or more solutions have a few errors but are understandable. Explanation may "flow" well but only vaguely explains one or more problems. Some parts of one or more solutions are difficult to follow. May include improper use of mathematical notation. | The presentation style is attractive but doesn't enhance the content; more flashy than functional. It is clear that the student has invested some effort into planning their presentation. |
| Journeyperson | Not all the problems are "routine" in nature. They span an appropriate breadth of material. At least one problem requires careful thought such as consideration of a special case or combines concepts from more than one unit. Showcases the writer's skill in solving routine mathematical problems. | All solutions are correct and easy to understand. Very few or no minor errors. Explanation "flows" well and explains the problems step by step. Solution is broken down well and explained in a way that makes it easy to follow. May have minor use of improper mathematical notation. May point out other ways of solving one or more problems as well. | The presentation may use multiple media tools. The presentation style is attractive and maintains interest. Some of the underlying message may be lost by some aspects that are more flashy than functional. It is clear that the student has given some forethought and planning to their presentation. |
| Expert | Problems span more than one unit worth of material. All problems are non-routine. Every problem includes content from at least two different units. Problems created demonstrate mastery of the subject matter. Showcases the writer's skill in solving challenging mathematical problems. | All solutions correct, understandable and highly detailed. No errors. Explanation "flows" well, explains the problems thoroughly and points out other ways of solving at least two of them. | The presentation displays use of multiple media tools. The presentation style grabs the viewer's or reader's attention and compliments the content in a way aids understanding and maintains interest. An "eye opening" display from which it is evident that the student invested significant effort. |
Creativity (up to 5% bonus)
The maximum possible mark for this assignment is 105%. You can earn up to 5% bonus marks for being creative in the way you approach this assignment. This is not a rigidly defined category and is open to interpretation. You can earn this bonus if your work can be described in one or more of these ways:
 Then, Richard took the role of “teacher” and moved us onto the next slide and enlarged the equations for all of us to see. Then, unknowingly, Mr. K. popped his head into the class and said at anytime we could put our answers on the board. Simultaneously, the class burst out into laughter because we were one step ahead of him. After that we clued him in on what was going on and he explained to us that the questions on the board were a bit different from the previous ones.
Then, Richard took the role of “teacher” and moved us onto the next slide and enlarged the equations for all of us to see. Then, unknowingly, Mr. K. popped his head into the class and said at anytime we could put our answers on the board. Simultaneously, the class burst out into laughter because we were one step ahead of him. After that we clued him in on what was going on and he explained to us that the questions on the board were a bit different from the previous ones.
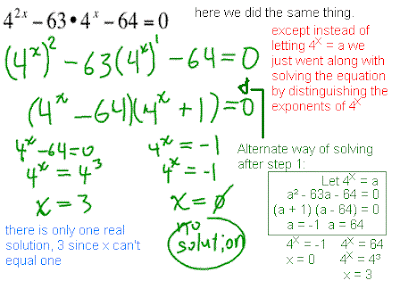




Just some of the possibilities of writing 2 exponentially. From writing these possibilities, we began to uncover a pattern to determine how to write a number in different ways using exponents. This pattern can be seen through the 81/3 which is equivalent to (1/8)-1/3. Using such examples can show that when we write any number to an exponent x, we can also write the reciprocal of that number to the exponent negative x.
From writing these values we further elaborated upon the aforementioned pattern. Then we quickly continued writing all of the possibilities for the next number, 4/9.
At this point, Mr. K asked if there were any ways we could come up with numbers with exponents that do not include the number 1. For exponents which do not contain 1, such as the exponent 2/3, this simply means that we must square both the numerator and denominator (if the base is a fraction) then take the cube root of both. For the exponent -2/3, we simply take the reciprocal of the base then apply the exponent 2/3.
At last, we wrote down some possibilities for the number 1/4. Another pattern emerged, concerning the number 1/4, this pattern was shown by the expressions (1/8)2/3, (1/32)2/5. This pattern seems to always have 2 as a numerator in the exponent, but increases by odd intervals for the denominator. As for the denominator of the base, it increases by a certain exponent, then is divided by 2. This pattern along with the other can help us when trying to write two numbers with the same base, which will be described in a little bit.
After we were done with all of those, and now that we knew there are an infinite number of ways to write any number using exponents, we moved on. But all of this was a great preparation for our real lesson for today. Solving the following equations:
2x = 64
272x-1 = 3
3x = 1/27
He taught us that we must solve these by making the bases equal to each other. If you set them equal to each other, since the bases are equal, they must equal the same number in the end, meaning that the exponents must also be equal. So if you set the bases equal, you can determine an unknown exponent since they must be equivalent. This is what we must know for this unit, as this is how we will perform and carry out logarithmic expressions.
Such as for the equation 2x = 64, we can solve this numerous ways, but as Mr. K said, and as we have learned before, we must set the bases equal to each other. The two most obvious ways to do so are as follows:
The above also states what to do in each step, although there are bound to be more complex problems in the future, leading to more steps. But each of the above show the basic structure for solving these equations; rewrite the equation with equal bases then you can get rid of the bases and set the exponents equal to each other. But remember, such as in the second example, make sure you keep the x when you alter the exponent if the x is in that exponent. Such as in 64(1/6)x, when the 2x was changed to a power to the base of 64, the x must still remain. Don't just change it to 641/6.
As for the other equations, the same mechanism was used for each solution, so just remember that if the bases are the same, then the exponents must also equal each other.
The work for each equation can be seen here.
Wednesday Afternoon:
In the afternoon class, we didn't learn anything as the afternoon was marked by a workshop concerning racism. In class we just talked about certain events, and Mr. K read out a story of which he was given to conduct the workshop. We began talking about incidents, and certain stories which pertained to the subject, and most of what we talked about in class can probably be found on the podcast. And that's about all I can say for now, as I'm running out of time.
Well that's my scribe everybody! Sorry if it came up late, I've already went back and forth with practicing for talent show and now my parents are angry with me so I have to cut this short. I won't have much time to edit this and even entirely complete it, so I'll be adding more to this post maybe later tonight or tomorrow, sorry for the inconvenience. If there's any mistakes, complaints, or anything whatsoever, just tell me, I still have to edit much of this post. I hope my scribe is useful to anyone that didn't attend class and it's at least sufficient considering the high standards on our blog. See you all tomorrow! OH and one last thing... the scribe for tomorrow will be...
Craig
Have a good night everyone! Don't forget to do your homework!

The geese who inhabit the wildlife preserve where we walk each day are back; not many, but a few as the ice begins to melt. I wonder if you see them yet, returning for spring flying along in "V" formation? Do you know what science has discovered as to why they fly that way?
FACT 1 - As each Goose flaps its wings it creates uplift for the birds that follow. By flying in a V formation, the whole flock adds 71 per cent greater flying range than if each bird flew alone.
FACT 2 - When a Goose falls out of formation, it suddenly feels the drag and resistance of flying alone. It quickly moves back into formation to take advantage of the lifting power of the bird immediately in front of it.
FACT 3 - When the lead Goose tires, it rotates back into the formation and another Goose flies to the point position.
FACT 4 - The Geese flying in formation honk to encourage those up front to keep up their speed.
FACT 5 - When a Goose gets sick, wounded or shot down, two Geese drop out of formation and follow it down to help and protect it. They stay with it until it dies or is able to fly again. Then, they launch out with another formation or catch up with the flock.
Are there lessons we can learn from a gaggle of geese? What do you think?


GOOD LUCK ON THE TEST AND PRETEST EVERYONE!! DON'T FORGET TO PRACTICE THOSE IDENTITIES!
Tags
The picture must be tagged properly with the course tag and assignment tag. If tags are misspelled or no tags are present the photo cannot be graded and will receive a grade of ZERO. Not tagging your photo properly and accurately is analogous to not handing in your work or not putting your name on it.
| Classification | Mathematical Content (50%) | Hot Spots (35%) | Photograph (15%) |
| Level 4 | Packed with mathematical concepts/facts. (Minimum 7 concepts/facts.) | All hot spots accessible; i.e. "smaller" hot spots are "on top" of larger ones, they do not obscure each other. All hot spots are actually labels and relate to parts of the photo (not on blank space with filled in notes). One or more hot spots include a link to a relevant supporting resource on the internet. Minimum 7 hot spots. | In focus or appropriately focused for effect. The subject of the picture occurs "naturally," it is not a contrived shot. Really makes the viewer "see" math in a place they hadn't realized it existed. (Example: trigonometry) |
| Level 3 | Significant number of concepts/facts included. (Minimum 5 concepts/facts.) | All hot spots accessible. Most hot spots are actually labels and relate to parts of the photo. Not more than one hot spot on blank space. One or more hot spots may include a link to a relevant supporting resource on the internet. Minimum 5 hot spots. | In focus or appropriately focused for effect. The subject of the photo has been "set up" or contrived yet still illustrates math found in "the real world." (Example: derivative) |
| Level 2 | Some effort to include content evident. (Minimum 3 concepts/facts.) | Most hot spots accessible. Most hot spots are actually labels and relate to parts of the photo. More than one hot spot is on "blank" space. May or may not include links to relevant supporting resource on the internet. Minimum 3 hot spots. | In focus or appropriately focused for effect. Although it is a "real world" picture, objects have been used to "draw" the math. An obviously contrived shot. (Example: trigonometry) |
| Level 1 | Very scarce content related to assignment. | Less than three hot spots are visible or have information related to the theme of the assignment. | It is evident that little effort went into finding and shooting a picture that reflects the theme of the assignment. |
| Level 0 | Content unrelated to theme of assignment. | No hot spots or mostly unrelated to the theme of the assignment. | Out of focus and/or otherwise difficult to look at. |
Creativity (up to 5% bonus)
The maximum possible mark for this assignment is 105%. You can earn up to 5% bonus marks for being creative in the way you approach this assignment. This is not a rigidly defined category and is open to interpretation. You can earn this bonus if your work can be described in one or more of these ways:
 | The early bird catches the worm... So I decided to do my BOB while I am still unable to sleep... So this unit will be a challenge for me, partly because I wasn't in class for 3 1/2 lessons. But I kinda understand |
| most of the things in it. There was Eddie and his very inspiring message to us from Georgia. The SINE dance is one of the main highlights of this unit. Well, there's Pi Day, where we ate at least 12 different kinds of pie. I have had enough pie for the whole year! Here are something's I learned: |

 Afterwards we all asked for an explanation.. hahaha… It’s so cool and funny when we do that…
Afterwards we all asked for an explanation.. hahaha… It’s so cool and funny when we do that…




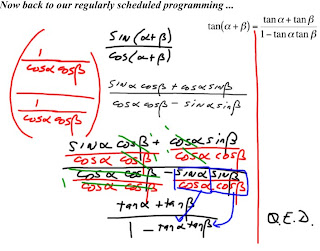



 This stating that we can use cos(2θ) to solve a multitude of questions.
This stating that we can use cos(2θ) to solve a multitude of questions.

