Morning Class:
We had a quiz on transformations. We went over the answers like we always do. Then, we started a lesson on Graphing Absolute Functions.
There are 2 easy steps used to graph an absolute function.
Step 1: Sketch the graph of y = f(x).
Step 2: Reflect all the parts of the graph below the x-axis over the x-axis.
Here's an example:
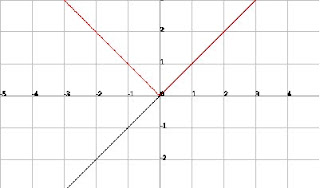.bmp)
The Black graph is the graph of y = x. The absolute value changes the negative output of the graph into a positive output. Where x<0, the negative outputs were changed to positive outputs.
Then, we looked at the graph of y=abs(2-x).
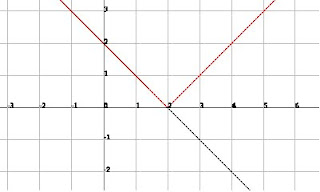.bmp) According to our steps, we need to graph y = 2-x first. Then, we reflected the negative inputs of this graph towards the x-axis to make them positive; as shown by the red graph.
According to our steps, we need to graph y = 2-x first. Then, we reflected the negative inputs of this graph towards the x-axis to make them positive; as shown by the red graph.That's all we did for the morning class.
Afternoon Class:
We looked at this graph:
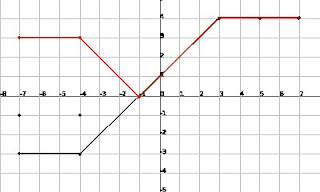 This graph has a function:
This graph has a function: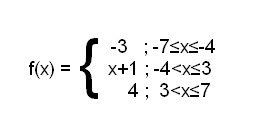 The Red graph shows the absolute value of the function. The black graph shows the original function.
The Red graph shows the absolute value of the function. The black graph shows the original function.Mr. K showed us how to graph this in our calculator. After researching and testing, (yay!) We were able to find the syntax to graph this in our calculator. Here's a small step-by-step procedure on how to graph this piecework:
Step 1: Press [Y=]
Step 2: Enter this syntax in "Y1"...
Y1 = (-3)(-7≤x)(x≤-4)+(x+1)(-4≤x)(x≤3)+(4)(3≤x)(x≤7)
Step 3: If there are "funky-looking" lines in your graph, press [Mode] then change "Connected" to "Dot". Press [Mode] again, then change it back to "Connected".
Mr. K also showed us how to graph the absolute value of this function. Here are the steps:
Step 1: Go back to the syntax entered in [Y1].
Step 2: Press [2nd] [Del] for "Insert".
Step 3: Press [MATH], then press [->] to go to "NUM".
Step 4: Press [1] for the "abs(" command.
Step 5: Place the cursor to the end of the syntax, then press [ ) ].
Your [Y1] should look something like this...
abs((-3)(-7≤x)(x≤-4)+(x+1)(-4≤x)(x≤3)+(4)(3≤x)(x≤7))
Then ♫TA-DA♫! Wicked awesome cool eh?
Then we looked at the graph of f(x) = abs(x^2-4)...
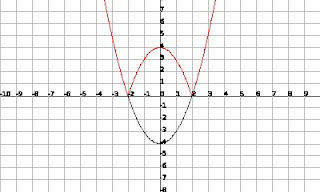 The part of the graph that is located below the x-axis was reflected along the x-axis.
The part of the graph that is located below the x-axis was reflected along the x-axis.Note: Watch out for the concavity (opens up or down) when graphing. We need to make sure the concavities of the graphs are properly drawn.
Then, we did a little bit of review regarding the Reciprocal Functions.
1. Given y = f(x), sketch the graph of y = 1/f(x).
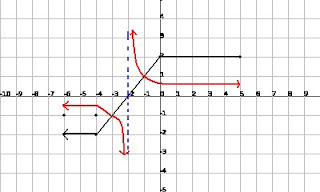 According to our rules, first find the "Invariant Points". Then, we find the asymptote(s), where the original graph has a root. Then we play the "Smallering & Biggering Game".
According to our rules, first find the "Invariant Points". Then, we find the asymptote(s), where the original graph has a root. Then we play the "Smallering & Biggering Game".Finally, we looked at the reciprocal graph of f(x) = 2sinx...
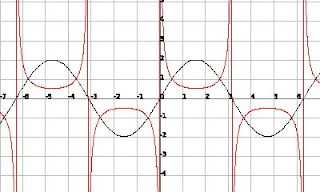 If you got the graph of 1/(sin(x)), the invariant points are connected to the minimums and maximums of the graph. In this case, the graph of 2sin(x) stretches the graph 2 units. The asymptotes are located at k"pi".
If you got the graph of 1/(sin(x)), the invariant points are connected to the minimums and maximums of the graph. In this case, the graph of 2sin(x) stretches the graph 2 units. The asymptotes are located at k"pi".That's all we did today! This post should have been posted earlier, but I had a few disturbances.
Oh yeah! JENG is the next scribe.☺

6 comments:
Hey Jann, you mentioned, "The absolute value changes the negative input of the graph into a positive input. Where x<0, the negative inputs were changed into positive inputs." I thought it was the outputs or the y-values that become positive. Let's say it's y = |x| and we substitute -3 to x. Wouldn't y become 3 and not x since it's -3? So the new coordinates would be (-3,3). I may not be making any sense at all. But I thought I learned that it's the y-values that become positive on an aboslute value graph. Also if we look at y = |2x+4|. If x = -2, then y would be 2(-2) + 4 = 0, and not 2(2) + 4 = 8. I don't know if I make sense here but in the first solution, we substitute -2 for x and not |-2| for x. Therefore, it is the y values or OUTPUTS that turn into positive values on absolute value functions when they were negatives to begin with. I hope you get me and I'm not sure if I'm making sense. Tell me if I learned it wrong. Thanks!
Great post though! It's concise and comprehendable! It's just that one little area where I got perplexed.
Yes you're right Vince! Sorry about that, I guess I got carried away. XD Thanks for noticing the error. OUTPUTS are the ones changed to positive, not the inputs (x values).
I was right? WOW I really thought I didn't make any sense.
good job on the post..I like the detail you put into graphing those functions on the calculator...clever title as well =)
Great post and good eye Vincent
Post a Comment