 As your scribe for today, I will put my efforts into defining today's lesson. I hope that standards will be met and that this may be used to a greater extent as a future reference.
As your scribe for today, I will put my efforts into defining today's lesson. I hope that standards will be met and that this may be used to a greater extent as a future reference.Today, we learned more about trig functions. We learned how to sketch the graphs, interpret the information, and undo our steps to either find equations from analyzing the graph or vice versa. There were many things that we went over today, upon which I will try to re-explain.
Class 1: Morning
To start the class off, we put our thoughts into questions that were written on the board.
1.) On the same cartesian plane, using 2 different colours, sketch at least 2 cycles of:
f(x) = Cos(x) and g(x) = Sin(x)

As Mr. K stated during the class, graphing these functions are as easy as counting from 1-4. In this example, upon which the graph is in intervals of Π/2, you would label your scale as Π/2, Π, 3Π/2, and 2Π on the positive side of the x-axis. On the negative side of the x-axis, you would label the scale with the same values except that they are negative: -Π/2, -Π, -3Π/2, and -2Π.
There are things to remember when graphing in order to achieve full marks. Some of which are quite simple:
- label your axis
- add arrows to your axis and your curves
- **make certain that the curve arrows either point up or down, NOT STRAIGHT
Back to the question, there are things that you should notice about the function of Sin(x) and Cos(x).
- both "wrap" around a line, known as the "sinusoidal axis" or the "average value of the function"
- Cosine starts at its max value
- Sine starts at its sinusoidal axis
Exploring further into the concept, we find that we can rewrite the function of Sin(x) in terms of Cosine, and rewrite the function of Cos(x) in terms of Sine.
Sin in terms of Cos:
-> Cos(x- Π/2) = Sin(x)
Cos in terms of Sin:
-> Sin(x+ Π/2) = Cos(x)
NOTE: Π/2 in both of these equations are the phase shift a long the horizontal axis, either left or right, depending on its sign, which will be discussed further on in this post.
2.) Without using a calculator, sketch each of the following graphs:
a.) y = Sin(x) - 1

b.) y = -2Sin(x)
Notice that the amplitude, in this case (2) is not negative because amplitudes are described as distances and therefore should not be negative.

c.) y = 2Sin(x) + 1

In graphing these functions, there are certain steps that may be followed to help make graphing easier also explained later in this post.
- - - - - - - - - -
-In general or standard form, the equation of sine functions are:
- f(x) = ASinB(x-C) + D
-Cosine is affected by the same transformations:
- f(x) = ACosB(x-C) + D
A- The value of A relates both to the amplitude and whether the function will be inverted or not over the y-axis. The amplitude (which is the absolute value of A: |A|) of the graph is the distance from the sinusoidal axis. Its sign influences whether the curve will "flip" over the y-axis or if it retains its normal position. Further explained later on.
B- Parameter B is not the period of the graph but helps determine the period. This is also explained further into the class.
C- The phase shift/ horizontal shift of the graph.
D- Parameter D is the sinusoidal axis, average value of the function, or the vertical shift.
- - - - - - - - - -
Now, having discovered the properties of the transformations, we dive deeper into the concept and talk about how these variables effect the graph and how graphing can be put into an easier form of remembering.
Ex. Sin2x
- the value of "B" causes "everything to happen twice as fast"
- the angle is "doubled" before finding the value of sine
Ex. Sin-2x
- Inputs are made negative first
- Note: x-coordinates are changing sign
- Note: the negative signs do not flip the graph vertically over the x-axis but horizontally over the y-axis
Now diving even deeper with this new knowledge, we compare more examples to notice occurring patterns (mathematics is the study of patterns). We do this by observing sketches of functions.
Sinx = 1/2 <-- 1 wave between 0-2Π
Sin2x = 1/2 <-- 2 waves between 0-2Π
Sin3x = 1/2 <-- 3 waves between 0-2Π Sin4x = 1/2 <--4 waves between 0-2Π So, we find that the value of "B" is somehow related to the number of waves between a given interval (in this case 0-2Π). However, when the word "Period" comes to mind, people ask themselves, is the value of "B" in fact the period? The answer to that is no. "B" is in fact not the period of the graph, but indeed helps determine it.
- A period is the distance of a hill and a wave.


Using this mode of representation, we can find the relationship between the value of "B" and the period.
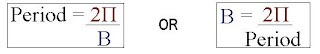 Now discovering all of this in the first class of the day may be quite a load. However, one thing that should definitely not be forgotten is the concept of the mnemonic: DABC. At first, the abbreviation may look unfamiliar. However when you peer closer, you notice that A, B, C, and D, are part of the transformational equation of Sine and Cosine! DABC is actually that, except in the form of order upon which can be helpful in remembering how to sketch trig functions.
Now discovering all of this in the first class of the day may be quite a load. However, one thing that should definitely not be forgotten is the concept of the mnemonic: DABC. At first, the abbreviation may look unfamiliar. However when you peer closer, you notice that A, B, C, and D, are part of the transformational equation of Sine and Cosine! DABC is actually that, except in the form of order upon which can be helpful in remembering how to sketch trig functions.D - Is the first step in sketching the graph of a trig function. D is the vertical shift or sinusoidal axis of the graph and should be found first, as you should know that the graph "wraps" around the sinusoidal axis.
A - Is the second step in sketching the graph of a trig function. A is the amplitude and determines the stretch of the graph. Also important about the amplitude is its sign. If it is negative, the graph appears to be inverted; it flips horizontally over the y-axis. If positive, Sine graphs will start at zero, and Cosine graphs will start at its max value, which is one.
B - Is the third step in sketching the graph of a trig function. B represents a factor that influences the period of the graph. This is used to determine the scale values of the x-axis.
C - Last but not least, the last step in sketching the graph of a trig function. C represents the horizontal shift of the graph.
When thinking of graphing one of these monsters, you may curse in the form of DABC (pronounced: Dah - Bick!). Then all of a sudden, a flash of insight washes over you and you suddenly remember how to sketch the graph! Isn't that amazing everyone?
Finally, we reached the last couple minutes of a long class (or short?). Mr. K put up an example, which he ended up sketching quickly on the board:
y= -3Cos2(x - Π/4) + 1

For indication purposes, during the class, Mr. K compared graphing trig functions to the "etchisketch" which is quite the analogy. He stated that one dial of the etchisketch could be compared to Sin and the other dial could be compared to Cos. Imagine both of the dials being turned simultaneously and the result is quite frankly circular functions displayed in a graphical manner or atleast visual.
Class 2: Afternoon
We started off the afternoon by taking a look at these two previous equations:
f(x) = AsinB(x-C)+D
f(x) = AcosB(x-C)+D
Discussing briefly about the two, we move quickly to an example.
Ex. y = -2sin3(x+Π/6)+1
- Note: The vertical shift is to the left in this example. The positive sign is due to a negative value input replacing the variable C. Since the formula has a negative sign, and the example has a positive sign, the horizontal shift is to the left because a (-)(-) = (+).
- Note: When solving this equation, for any reason, simply use the order of operations: BEDMAS

Now having graphed this function, Mr. K talked brought up a great topic. He said that, if you know how to do something one way in math, you should know how to undo it. So, that's what we ended up doing. Instead of converting the equation to a graphical mode of representation, we reversed the method and converted the graphs into symbolic modes of representation: in the form of an equation.
So you might ask, how do you do that? Well, we started off by find the values ABCD of the transformational equations of sine or cosine.
Note: For this one graph, there can be a large (when I say large, I mean LARGE) quantity of equations that when graphed, will all look similar or are exact replicates.
We decided to rewrite the equation in Cosine:
- A= -2
- B= 3 (B= 2
 Π/p = 2Π/2Π/3 = 3)
Π/p = 2Π/2Π/3 = 3)
- C= 0 (normal cosine curves start at its max, whiel this graph starts at its min due to the negative amplitude sign)
- D= 1
y=-2cos3x+1
Next we decided to rewrite the equation 3 more times: 2 in terms of cosine, and 1 in terms of sine.
Sine
- A= 2
- B= 3
- C= Π/6
- D= 1
Cosine1
- A= 2
- B= 3
- C= -Π/3
- D= 1
Cosine2
- A= 2
- B= 3
- C= -Π/3
- D= 1
After all those nice examples, we look at where the quadrants are located in the graph. To put it short, depending on where your starting point is, the period of the curve is divided by 4 pieces, quadrant 1, 2, 3, and 4 before repeating itself again.
 After this, we quickly went over number 15 of exercise #5, and number 12 of exercise #6.
After this, we quickly went over number 15 of exercise #5, and number 12 of exercise #6.We are now DONEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEE the unit and our pretest is on its way (supposedly thursday). Tomorrow, we are taking notes into our super duper "Math Dictionary of Power" (lol) and are going over any issues, concerns, and questions about the unit! Make sure to ask some questions or we'll just have wasted a class that could've been used towards our exam studying time near the end.
WOW THAT WAS A DOOZY. Now we near the end.
Any comments, suggestions, error fixing, criticism, appreciation, is accepted :)
Homework for tonight: Curve sketching posted by Mr. K (so far has not appeared)
Scribe for tomorrow: Bertman! (sorry Sam, Bert asked me first :P)
Have a nice day. Night.

29 comments:
Good job Timmy, I really like your graphics and use of colour! Everything was very detailed. =)
thanks! =)
Good job, Timmy! Way to go! This might have take a whole night of games?! haha. Anyway, very small amount of grammatical error and the fact that Mr. K. recommended not to use arabic values to indicate the quadrants. Use roman numerals instead. Overall, it rocks! HAHA! I'm just curious where you happened to construct those perfect graphs. It would hasten a lot of our fellow bloggers because they're easier to make instead of drawing them free-handedly. Good job again and see you tomorrow!
wows thanks man! lol i forgot about the roman numerals for quadrant numbering.. bah! well i got the idea from mr.k when i asked him how to make quick graphs. mr.k showed me the link on our blog called "Mathematics Archives" where mr.k dug through to find me a list of programs to use. i asked john about it and he perscribed me graphmatica. i downloaded and used it :), with the help of john and richard to answer questions about it
http://archives.math.utk.edu/software/msdos/
graphing/grmat/.html
Graphmatica, download windows version, its an excellent program.
I'm speachless. Ver niice job. *claps*
;)
lol now i know about DABC
--sheep
SHEEP! you are here! i never see you on anymore. oh so lauressa isnt a big jello after all. haha. hi sheep =)
I suggest Timmy's scribe post is inducted to the Hall of Fame because of the fact that the post entails every detail involved in yesterday's class. Not only that, he also clarified some confusing points. His images and text both contribute to the quality of the post.
I second Vincents motion to have this inducted into the H.o.F. because of the enormous amount detail this post contains. GJ Timmy.
wow awesome i got 2! ty
I cast my vote that Tim-MATH-y's scribe post be inducted into the hall of fame because it was very detailed and the use of graphs was very helpfil.
Hello Mathy Tim!
I also think your post is great. I only now had a chance to read it and I don't know if I can vote, but I'd certainly vote for Hall of Fameness :) I still have to do my job, which is to ask questions.
1. What is the difference between:
a) f(x)=2sin(3)x+5
b) g(x)=2sin(3x)+5
c) h(x)=2sin3x+5?
2. You said: "A- The amplitude of the graph is the distance from the sinusoidal axis. Its sign indicates whether the function will be inverted or not over the x-axis, further explained later on in the class."
Elsewhere in the post you said that A can not be negative as it describes the distance. Let's consider
f(x)=-7sin(3x+pi/3)+2
What are A, B, C and D in this example?
I'll wait for response and further discussion :)
e
I also think this post should be inducted into the hall of fame because of the graphics, use of colour incorporated with in the post, and I find I can understand it.
WoW, great questions. I guess I should try to the best of my abilities to answer them for you.
1.) Well from the looks of these functions, and considering that this question seems quite difficult for me to explain, I do believe that they all seem quite similar, in respect to how they would be drawn on the same cartesian plane. However, I believe there might be more of a twist to these examples.
a) f(x)=2sin(3)x+5
b) g(x)=2sin(3x)+5
c) h(x)=2sin3x+5?
2.) I was quite uncertain when pondering about this concept.
A= -7
B= 3
C= pi/9
D= 2
f(x)=-7sin(3x+pi/3)+2
f(x)=-7sin3(x+pi/9)+2
Now, taking this information in, I notice that my post has a minor error. The value of "A" is not the amplitude. However, the value of |A| is the amplitude, and I believe that is should answer your question.
Well correct me or discuss upon what you think about my thoughts. =)
Hi Tim Math y,
Congratulations on an examplary scribe!
Your detailed explanations and graphics contributed to the understanding of the content. In addition, you collaborated to reach this excellence, and your post generated such a great discussion.
I'd like to offer a "Hall of Fame" worthy!
Best,
Lani
All I can do right now is:
=)
Hi Tim,
I like how you handled 2. I agree that we should allow A to be negative, and that its absolute value is the amplitude. Nice job.
Let's talk about 1. Here are the functions:
a) f(x)=2sin(3)x+5
b) g(x)=2sin(3x)+5
c) h(x)=2sin3x+5?
You remember discussion about input and output of functions with grey-m? That is what the differences above are all about. I can rewrite the functions so that it would be clearer:
a)f(x)=2sin(3)x+5 = 2*sin(3)*x+5 =
= (2*sin(3))x+5,
so f is really just a linear function with slope 2sin(3) and y-intercept 5. See, here the input for sine is 3, not 3x (that's why there are parentheses there).
b)g(x)= 2sin(3x)+5
is what you wanted to have, a trig function with A=2, B=3, C=0 and D=5.
c)h(x)=2sin3x+5
I can't tell. I would say that it's same as f, but I think you wanted it to be same as g. It is in this case ambiguous as to what the input for the sine function is.
What do you think?
Tim,
One more thing. In 2. is C pi/9 or -pi/9?
I hope you're still smiling because you're doing an awesome job :)
e
Let me add my vote to make it 7 so far. ;-)
I think this post deserves to be in the Hall Of Fame not only for all the reasons people before me have mentioned, but also for the conversation that has evolved in the comments. The difference between y=sin(3)x and y=sin(3x) and the ambiguity in expressions like y=sin3x may seem small but are quite significant. As e has pointed out, one is a line and the other is a wave the last is ...? Very different functions.
You've heard me say "learning is a conversation" ... this is a real learning conversation. Keep it up! ;-)
Haha!
Well, for starters, I knew there was a twist with those examples! Especially example(a) of question 1 because I actually graphed all three of the functions and found that it was linear. That put quite the suspicion in my mind but I did not quite know how to explain what I was seeing.
Thank you for pointing out the differences of the three examples, It definitely filled some gaps.
Now for number 2.. hrm.. I think that you are trying to hint upon something about this question.
Trusting my thoughts, I believe that.. OH! FLASH OF INSIGHT! yes C= -pi/9 since the example shows: x+pi/9 and the equation is x(MINUS)C.
Therefore, (-)(-) cancel out to give + result!
Yes, C= -pi/9.. bah how'd I mess up to start.. :P
Oh, I totally forgot to vote tim-math-y's scibe into the hall of fame. Ok I formally want to vote tim-math-y's scribe into the hall of fame because of his excellent details on solving each and every question and his excellent visuals and finally for his rational to be able to do the scribe while avoiding video games. Excellent Work Tim-Math-Y
Well, I would have to say HALL OF FAME!!! I really got to experience the full use of the Scribe Post. I was not present for this class, but I really felt I was "there" after reading this scribe. The explanations were so detailed and were exactly how I think Mr. K. would present them. The graphics were stunning and the work was displayed nicely. Plus it was about as long as a Math class anyways. LOL
Wow, I just counted, Tim-Math-y is in the 'Scribe Hall of Fame' with 9 votes!!!
You graphed the functions I gave you? Nice job, I wouldn't have thought to do that. I learned something, too. Use technology more often :) But I am definitely glad that you wanted an explanation, too! We'll talk more, I'm sure.
Nice! Thank you all for voting my scribe post into the Hall of Fame! (Hononored). Wow, 26 comments! Awesome!
=)
Hey! I don't know why you have made this blog thing, but I'm a trigonometry student and the way my teacher tries to teach us trig just is NOT working. And i googled some of it to get some definitions and your blog just made EVERYTHING click. GAH thank you SO much, sosososo much. This is amazing and I'm going to ace my next test cuz of you.
Wow! I don't know much to say! I'm glad that my scribe post has really enriched your knowledge of trig!
Knowing that my scribe post has helped someone like you really makes me feel great =). Thanks!
Goodluck on your test!
Post a Comment